Graphs of trig functions  (Page 102/2)

History of trigonometry

Work in pairs or groups and investigate the history of the development of trigonometry. Describe the various stages of development and how different cultures used trigonometry to improve their lives.

The works of the following people or cultures can be investigated:

1. Cultures
   1. Ancient Egyptians
   2. Mesopotamians
   3. Ancient Indians of the Indus Valley
2. People
   1. Lagadha (circa 1350-1200 BC)
   2. Hipparchus (circa 150 BC)
   3. Ptolemy (circa 100)
   4. Aryabhata (circa 499)
   5. Omar Khayyam (1048-1131)
   6. Bhaskara (circa 1150)
   7. Nasir al-Din (13th century)
   8. al-Kashi and Ulugh Beg (14th century)
   9. Bartholemaeus Pitiscus (1595)

Graphs of trigonometric functions

Functions of the form $y=sin\left(k\theta \right)$

In the equation, $y=sin\left(k\theta \right)$ , $k$ is a constant and has different effects on the graph of the function. The general shape of the graph of functions of this form is shown in [link] for the function $f\left(\theta \right)=sin\left(2\theta \right)$ .

Functions of the form $y=sin\left(k\theta \right)$

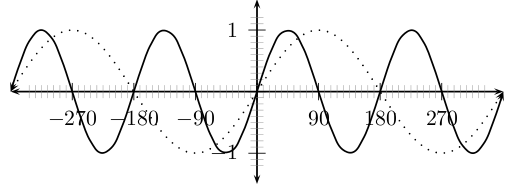
On the same set of axes, plot the following graphs:

1. $a\left(\theta \right)=sin0,5\theta$
2. $b\left(\theta \right)=sin1\theta$
3. $c\left(\theta \right)=sin1,5\theta$
4. $d\left(\theta \right)=sin2\theta$
5. $e\left(\theta \right)=sin2,5\theta$

Use your results to deduce the effect of $k$ .

You should have found that the value of $k$ affects the period or frequency of the graph. Notice that in the case of the sine graph, the period (length of one wave) is given by $\frac{{360}^{\circ }}{k}$ .

These different properties are summarised in [link] .

$k>0$	$k<0$

Domain and range

For $f\left(\theta \right)=sin\left(k\theta \right)$ , the domain is $\{\theta :\theta \in \mathbb{R}\}$ because there is no value of $\theta \in \mathbb{R}$ for which $f\left(\theta \right)$ is undefined.

The range of $f\left(\theta \right)=sin\left(k\theta \right)$ is $\left\{f\right(\theta ):f(\theta )\in [-1,1\left]\right\}$ .

Intercepts

For functions of the form, $y=sin\left(k\theta \right)$ , the details of calculating the intercepts with the $y$ axis are given.

There are many $x$ -intercepts.

The $y$ -intercept is calculated by setting $\theta =0$ :

Functions of the form $y=cos\left(k\theta \right)$

In the equation, $y=cos\left(k\theta \right)$ , $k$ is a constant and has different effects on the graph of the function. The general shape of the graph of functions of this form is shown in [link] for the function $f\left(\theta \right)=cos\left(2\theta \right)$ .

Functions of the form $y=cos\left(k\theta \right)$

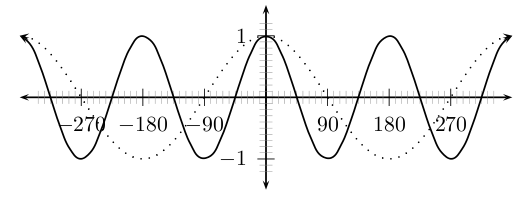
On the same set of axes, plot the following graphs:

1. $a\left(\theta \right)=cos0,5\theta$
2. $b\left(\theta \right)=cos1\theta$
3. $c\left(\theta \right)=cos1,5\theta$
4. $d\left(\theta \right)=cos2\theta$
5. $e\left(\theta \right)=cos2,5\theta$

Use your results to deduce the effect of $k$ .

You should have found that the value of $k$ affects the period or frequency of the graph. The period of the cosine graph is given by $\frac{{360}^{\circ }}{k}$ .

These different properties are summarised in [link] .

$k>0$	$k<0$

Domain and range

For $f\left(\theta \right)=cos\left(k\theta \right)$ , the domain is $\{\theta :\theta \in \mathbb{R}\}$ because there is no value of $\theta \in \mathbb{R}$ for which $f\left(\theta \right)$ is undefined.

The range of $f\left(\theta \right)=cos\left(k\theta \right)$ is $\left\{f\right(\theta ):f(\theta )\in [-1,1\left]\right\}$ .

Intercepts

For functions of the form, $y=cos\left(k\theta \right)$ , the details of calculating the intercepts with the $y$ axis are given.

The $y$ -intercept is calculated as follows: