| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
One formula you’ll use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant speed. The basic idea is probably already familiar to you. Do you know what distance you travel if you drove at a steady rate of miles per hour for hours? (This might happen if you use your car’s cruise control while driving on the Interstate.) If you said miles, you already know how to use this formula!
The math to calculate the distance might look like this:
In general, the formula relating distance, rate, and time is
For an object moving in at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula
where distance, rate, and time.
Notice that the units we used above for the rate were miles per hour, which we can write as a ratio Then when we multiplied by the time, in hours, the common units ‘hour’ divided out. The answer was in miles.
Jamal rides his bike at a uniform rate of miles per hour for hours. How much distance has he traveled?
| Step 1.
Read the problem.
You may want to create a mini-chart to summarize the information in the problem. |
|
| Step 2. Identify what you are looking for. | distance traveled |
| Step 3. Name. Choose a variable to represent it. | let d = distance |
| Step 4.
Translate.
Write the appropriate formula for the situation. Substitute in the given information. |
|
| Step 5. Solve the equation. | |
Step 6.
Check: Does 42 miles make sense?
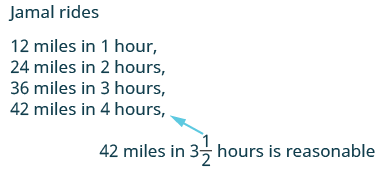 |
|
| Step 7. Answer the question with a complete sentence. | Jamal rode 42 miles. |
Lindsay drove for hours at miles per hour. How much distance did she travel?
330 mi
Trinh walked for hours at miles per hour. How far did she walk?
7 mi
Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of miles. If he can drive at a steady rate of miles per hour, how many hours will the trip take?
| Step 1.
Read the problem.
Summarize the information in the problem. |
|
| Step 2. Identify what you are looking for. | how many hours (time) |
| Step 3.
Name:
Choose a variable to represent it. |
let t = time |
| Step 4.
Translate.
Write the appropriate formula. Substitute in the given information. |
|
| Step 5. Solve the equation. | |
| Step 6.
Check:
Substitute the numbers into the formula and make sure the result is a true statement. |
|
| Step 7.
Answer the question with a complete sentence.
We know the units of time will be hours because we divided miles by miles per hour. |
Ray's trip will take 8 hours. |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?