1. Home
  2. General physics ii phy2202ca
  3. Geometric optics
  4. Image formation by lenses

9.6 Image formation by lenses  (Page 2/18)

<< Chapter < Page
  General physics ii phy2202ca     Page 2 / 18
Chapter >> Page >
P = 1 f . size 12{P= { {1} over {f} } } {}

Power P size 12{P} {}

The power P size 12{P} {} of a lens is defined to be the inverse of its focal length. In equation form, this is

P = 1 f . size 12{P= { {1} over {f} } } {}

where f size 12{f} {} is the focal length of the lens, which must be given in meters (and not cm or mm). The power of a lens P has the unit diopters (D), provided that the focal length is given in meters. That is, 1 D = 1 / m , or 1 m − 1 . (Note that this power (optical power, actually) is not the same as power in watts defined in Work, Energy, and Energy Resources . It is a concept related to the effect of optical devices on light.) Optometrists prescribe common spectacles and contact lenses in units of diopters.

What is the power of a common magnifying glass?

Suppose you take a magnifying glass out on a sunny day and you find that it concentrates sunlight to a small spot 8.00 cm away from the lens. What are the focal length and power of the lens?

Strategy

The situation here is the same as those shown in [link] and [link] . The Sun is so far away that the Sun’s rays are nearly parallel when they reach Earth. The magnifying glass is a convex (or converging) lens, focusing the nearly parallel rays of sunlight. Thus the focal length of the lens is the distance from the lens to the spot, and its power is the inverse of this distance (in m).

Solution

The focal length of the lens is the distance from the center of the lens to the spot, given to be 8.00 cm. Thus,

f = 8.00 cm.

To find the power of the lens, we must first convert the focal length to meters; then, we substitute this value into the equation for power. This gives

P = 1 f = 1 0 . 0800 m = 12 . 5 D. size 12{P= { {1} over {f} } = { {1} over {0 "." "0800"" m"} } ="12" "." 5" D"} {}

Discussion

This is a relatively powerful lens. The power of a lens in diopters should not be confused with the familiar concept of power in watts. It is an unfortunate fact that the word “power” is used for two completely different concepts. If you examine a prescription for eyeglasses, you will note lens powers given in diopters. If you examine the label on a motor, you will note energy consumption rate given as a power in watts.

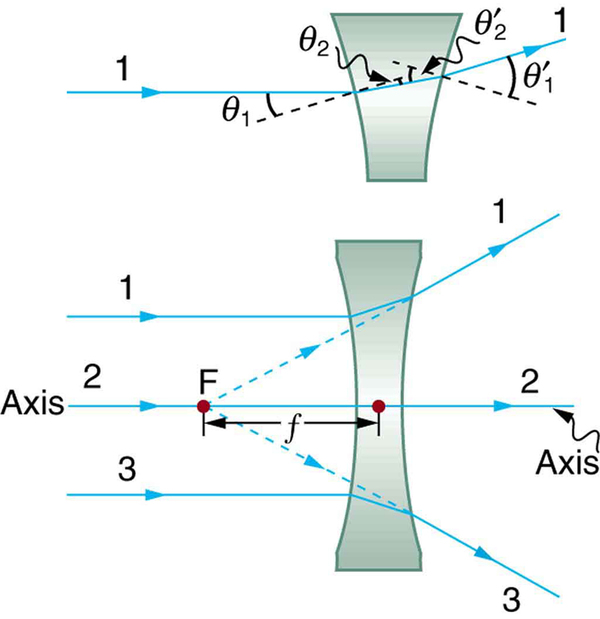
[link] shows a concave lens and the effect it has on rays of light that enter it parallel to its axis (the path taken by ray 2 in the figure is the axis of the lens). The concave lens is a diverging lens    , because it causes the light rays to bend away (diverge) from its axis. In this case, the lens has been shaped so that all light rays entering it parallel to its axis appear to originate from the same point, F size 12{F} {} , defined to be the focal point of a diverging lens. The distance from the center of the lens to the focal point is again called the focal length f size 12{f} {} of the lens. Note that the focal length and power of a diverging lens are defined to be negative. For example, if the distance to F size 12{F} {} in [link] is 5.00 cm, then the focal length is f = –5.00 cm and the power of the lens is P = –20 D size 12{P"=-""20"" D"} {} . An expanded view of the path of one ray through the lens is shown in the figure to illustrate how the shape of the lens, together with the law of refraction, causes the ray to follow its particular path and be diverged.

The figure on the top shows an expanded view of refraction for ray 1 falling on a concave lens. The angle of incidence is theta 1 and angle of refraction theta 2. The ray after the refraction at the second surface emerges with an angle equal to theta 1 prime with the perpendicular drawn at that point. Perpendiculars are shown as dotted lines. The figure at the bottom shows a concave lens. Three rays, 1, 2, and 3, are considered. Ray 2 falls on the axis and rays 1 and 3 are parallel to the axis. Rays 1 and 3 after refraction appear to come from a point F on the axis. The distance from the center of the lens to F is small f and is measured from the same side as the incident rays. Ray 2 on the axis goes undeviated.
Rays of light entering a diverging lens parallel to its axis are diverged, and all appear to originate at its focal point F size 12{F} {} . The dashed lines are not rays—they indicate the directions from which the rays appear to come. The focal length f size 12{f} {} of a diverging lens is negative. An expanded view of the path taken by ray 1 shows the perpendiculars and the angles of incidence and refraction at both surfaces.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 8

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, General physics ii phy2202ca. OpenStax CNX. Jul 05, 2013 Download for free at http://legacy.cnx.org/content/col11538/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'General physics ii phy2202ca' conversation and receive update notifications?

Ask