1. Home
  2. Une: physics for the health
  3. Unit 08 - impulsive force
  4. Collisions of point masses in

9.6 Collisions of point masses in two dimensions  (Page 4/5)

<< Chapter < Page
  Une: physics for the health     Page 4 / 5
Chapter >> Page >

Section summary

  • The approach to two-dimensional collisions is to choose a convenient coordinate system and break the motion into components along perpendicular axes. Choose a coordinate system with the x -axis parallel to the velocity of the incoming particle.
  • Two-dimensional collisions of point masses where mass 2 is initially at rest conserve momentum along the initial direction of mass 1 (the x -axis), stated by m 1 v 1 = m 1 v ′ 1 cos θ 1 + m 2 v ′ 2 cos θ 2 and along the direction perpendicular to the initial direction (the y -axis) stated by 0 = m 1 v ′ 1 y + m 2 v ′ 2 y .
  • The internal kinetic before and after the collision of two objects that have equal masses is
    1 2 mv 1 2 = 1 2 mv ′ 1 2 + 1 2 mv ′ 2 2 + mv ′ 1 v ′ 2 cos θ 1 − θ 2 .
  • Point masses are structureless particles that cannot spin.

Conceptual questions

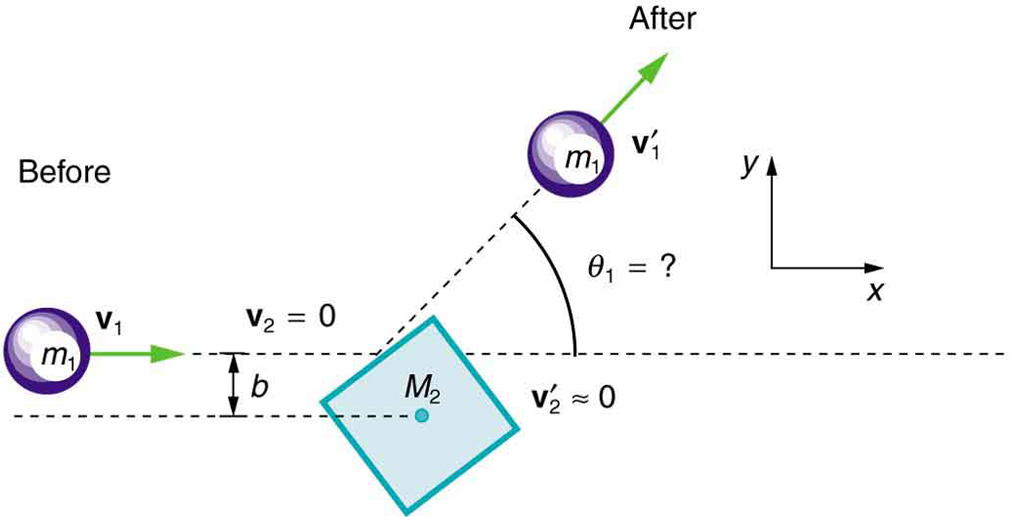
[link] shows a cube at rest and a small object heading toward it. (a) Describe the directions (angle θ 1 size 12{θ rSub { size 8{1} } } {} ) at which the small object can emerge after colliding elastically with the cube. How does θ 1 size 12{θ rSub { size 8{1} } } {} depend on b size 12{b} {} , the so-called impact parameter? Ignore any effects that might be due to rotation after the collision, and assume that the cube is much more massive than the small object. (b) Answer the same questions if the small object instead collides with a massive sphere.

A ball m one moves horizontally to the right with speed v one. It will collide with a stationary square labeled capital m two that is rotated at approximately forty-five degrees. The point of impact is on a face of the square a distance b above the center of the square. After the collision the ball is shown heading off at an angle theta one above the horizontal with a speed v one prime. The square remains essentially stationary (v 2 prime is approximately zero).
A small object approaches a collision with a much more massive cube, after which its velocity has the direction θ 1 size 12{θ rSub { size 8{1} } } {} . The angles at which the small object can be scattered are determined by the shape of the object it strikes and the impact parameter b size 12{b} {} .

Problems&Exercises

Two identical pucks collide on an air hockey table. One puck was originally at rest. (a) If the incoming puck has a speed of 6.00 m/s and scatters to an angle of 30 . 0º ,what is the velocity (magnitude and direction) of the second puck? (You may use the result that θ 1 − θ 2 = 90º for elastic collisions of objects that have identical masses.) (b) Confirm that the collision is elastic.

(a) 3.00 m/s, 60º below x size 12{x} {} -axis

(b) Find speed of first puck after collision: 0 = m v ′ 1 sin 30º − m v ′ 2 sin 60º ⇒ v ′ 1 = v ′ 2 sin 60º sin 30º = 5.196 m/s

Verify that ratio of initial to final KE equals one: KE = 1 2 mv 1 2 = 18 m J KE = 1 2 mv ′ 1 2 + 1 2 mv ′ 2 2 = 18 m J KE KE′ = 1.00

Confirm that the results of the example [link] do conserve momentum in both the x size 12{x} {} - and y size 12{y} {} -directions.

A 3000-kg cannon is mounted so that it can recoil only in the horizontal direction. (a) Calculate its recoil velocity when it fires a 15.0-kg shell at 480 m/s at an angle of 20 . 0º size 12{"20" "." 0°} {} above the horizontal. (b) What is the kinetic energy of the cannon? This energy is dissipated as heat transfer in shock absorbers that stop its recoil. (c) What happens to the vertical component of momentum that is imparted to the cannon when it is fired?

(a) − 2 . 26 m/s size 12{ - 2 "." "26"`"m/s"} {}

(b) 7 . 63 × 10 3 J size 12{7 "." "63" times "10" rSup { size 8{3} } `J} {}

(c) The ground will exert a normal force to oppose recoil of the cannon in the vertical direction. The momentum in the vertical direction is transferred to the earth. The energy is transferred into the ground, making a dent where the cannon is. After long barrages, cannon have erratic aim because the ground is full of divots.

Professional Application

A 5.50-kg bowling ball moving at 9.00 m/s collides with a 0.850-kg bowling pin, which is scattered at an angle of 85 . 0º size 12{"85" "." 0°} {} to the initial direction of the bowling ball and with a speed of 15.0 m/s. (a) Calculate the final velocity (magnitude and direction) of the bowling ball. (b) Is the collision elastic? (c) Linear kinetic energy is greater after the collision. Discuss how spin on the ball might be converted to linear kinetic energy in the collision.

Professional Application

Ernest Rutherford (the first New Zealander to be awarded the Nobel Prize in Chemistry) demonstrated that nuclei were very small and dense by scattering helium-4 nuclei ( 4 He ) from gold-197 nuclei ( 197 Au ) . The energy of the incoming helium nucleus was 8.00 × 10 − 13 J , and the masses of the helium and gold nuclei were 6.68 × 10 − 27 kg and 3.29 × 10 − 25 kg , respectively (note that their mass ratio is 4 to 197). (a) If a helium nucleus scatters to an angle of 120º during an elastic collision with a gold nucleus, calculate the helium nucleus’s final speed and the final velocity (magnitude and direction) of the gold nucleus. (b) What is the final kinetic energy of the helium nucleus?

(a) 5 . 36 × 10 5 m/s at − 29.5º

(b) 7 . 52 × 10 − 13 J size 12{7 "." "52" times "10" rSup { size 8{ - "13"} } `J} {}

Professional Application

Two cars collide at an icy intersection and stick together afterward. The first car has a mass of 1200 kg and is approaching at 8 . 00 m/s size 12{8 "." "00"`"m/s"} {} due south. The second car has a mass of 850 kg and is approaching at 17 . 0 m/s size 12{"17" "." 0`"m/s"} {} due west. (a) Calculate the final velocity (magnitude and direction) of the cars. (b) How much kinetic energy is lost in the collision? (This energy goes into deformation of the cars.) Note that because both cars have an initial velocity, you cannot use the equations for conservation of momentum along the x size 12{x} {} -axis and y size 12{y} {} -axis; instead, you must look for other simplifying aspects.

Starting with equations m 1 v 1 = m 1 v ′ 1 cos θ 1 + m 2 v ′ 2 cos θ 2 and 0 = m 1 v ′ 1 sin θ 1 + m 2 v ′ 2 sin θ 2 for conservation of momentum in the x - and y -directions and assuming that one object is originally stationary, prove that for an elastic collision of two objects of equal masses,

1 2 mv 1 2 = 1 2 mv ′ 1 2 + 1 2 mv ′ 2 2 + mv ′ 1 v ′ 2 cos θ 1 − θ 2

as discussed in the text.

We are given that m 1 = m 2 ≡ m size 12{m rSub { size 8{1} } =m rSub { size 8{2} } equiv m} {} . The given equations then become:

v 1 = v 1 cos θ 1 + v 2 cos θ 2

and

0 = v ′ 1 sin θ 1 + v ′ 2 sin θ 2 .

Square each equation to get

v 1 2 = v ′ 1 2 cos 2 θ 1 + v ′ 2 2 cos 2 θ 2 + 2 v ′ 1 v ′ 2 cos θ 1 cos θ 2 0 = v ′ 1 2 sin 2 θ 1 + v ′ 2 2 sin 2 θ 2 + 2 v ′ 1 v ′ 2 sin θ 1 sin θ 2 .

Add these two equations and simplify:

v 1 2 = v ′ 1 2 + v ′ 2 2 + 2 v ′ 1 v ′ 2 cos θ 1 cos θ 2 + sin θ 1 sin θ 2 = v ′ 1 2 + v ′ 2 2 + 2 v ′ 1 v ′ 2 1 2 cos θ 1 − θ 2 + 1 2 cos θ 1 + θ 2 + 1 2 cos θ 1 − θ 2 − 1 2 cos θ 1 + θ 2 = v ′ 1 2 + v ′ 2 2 + 2 v ′ 1 v ′ 2 cos θ 1 − θ 2 .

Multiply the entire equation by 1 2 m size 12{ { { size 8{1} } over { size 8{2} } } m} {} to recover the kinetic energy:

1 2 mv 1 2 = 1 2 m v ′ 1 2 + 1 2 m v ′ 2 2 + m v ′ 1 v ′ 2 cos θ 1 − θ 2

Integrated Concepts

A 90.0-kg ice hockey player hits a 0.150-kg puck, giving the puck a velocity of 45.0 m/s. If both are initially at rest and if the ice is frictionless, how far does the player recoil in the time it takes the puck to reach the goal 15.0 m away?
<< Chapter < Page Page > Chapter >>
Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Une: physics for the health professions. OpenStax CNX. Aug 20, 2014 Download for free at http://legacy.cnx.org/content/col11697/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Une: physics for the health professions' conversation and receive update notifications?

Ask