9.5 Practice 1: confidence intervals for averages, known population

$\overline{x}=$

$n$ =

15=(insert symbol here)

Define the Random Variable, $\overline{X}$ , in words.

$\overline{X}$ =

What is $\overline{x}$ estimating?

Is ${\sigma }_x$ known?

As a result of your answer to (4), state the exact distribution to use when calculating the Confidence Interval.

How much area is in both tails (combined)? $\alpha =$ $\text{\_\_\_\_\_\_\_\_}$

How much area is in each tail? $\frac{\alpha }{2}=$ $\text{\_\_\_\_\_\_\_\_}$

Identify the following specifications:

• a lower limit =
• b upper limit =
• c error bound =

The 95% Confidence Interval is:__________________

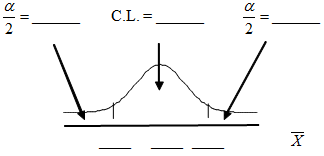
In one complete sentence, explain what the interval means.

Using the same mean, standard deviation and level of confidence, suppose that $n$ were 69 instead of 25. Would the error bound become larger or smaller? How do you know?

Using the same mean, standard deviation and sample size, how would the error bound change if the confidence level were reduced to 90%? Why?