8.1 Applications of trig functions (2d & 3d), other geometries  (Page 3/2)

Applications of trigonometric functions

Problems in two dimensions

For the figure below, we are given that $BC=BD=x$ .

Show that $B{C}^2=2x^2(1+sin\theta )$ .

1. Identify a strategy

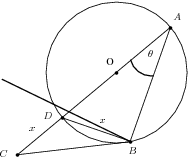
   We want $CB$ , and we have $CD$ and $BD$ . If we could get the angle $B\widehat{D}C$ , then we could use the cosine rule to determine $BC$ . This is possible, as $▵ABD$ is a right-angled triangle. We know this from circle geometry, that any triangle circumscribed by a circle with one side going through the origin, is right-angled. As we have two angles of $▵ABD$ , we know $A\widehat{D}B$ and hence $B\widehat{D}C$ . Using the cosine rule, we can get $B{C}^2$ .

2. Execute the strategy
   $$A\widehat{D}B={180}^{\circ }-\theta -{90}^{\circ }={90}^{\circ }-\theta$$

   Thus

   $$\begin{array}{ccc}\hfill B\widehat{D}C& =& {180}^{\circ }-A\widehat{D}B\hfill \\ & =& {180}^{\circ }-({90}^{\circ }-\theta )\hfill \\ & =& {90}^{\circ }+\theta \hfill \end{array}$$

   Now the cosine rule gives

   $$\begin{array}{ccc}\hfill B{C}^2& =& C{D}^2+B{D}^2-2·CD·BD·cos\left(B\widehat{D}C\right)\hfill \\ & =& x^2+x^2-2·x^2·cos({90}^{\circ }+\theta )\hfill \\ & =& 2x^2+2x^2\left[,sin,\left({90}^{\circ }\right),cos,\left(\theta \right),+,sin,\left(\theta \right),cos,\left({90}^{\circ }\right)\right]\hfill \\ & =& 2x^2+2x^2\left[,1,·,cos,\left(,\theta ,\right),+,sin,\left(,\theta ,\right),·,0\right]\hfill \\ & =& 2x^2(1-sin\theta )\hfill \end{array}$$

1. For the diagram on the right,
   1. Find $A\widehat{O}C$ in terms of $\theta$ .
   2. Find an expression for:
      1. $cos\theta$
      2. $sin\theta$
      3. $sin2\theta$
   3. Using the above, show that $sin2\theta =2sin\theta cos\theta$ .
   4. Now do the same for $cos2\theta$ and $tan\theta$ .

   

2. $DC$ is a diameter of circle $O$ with radius $r$ . $CA=r$ , $AB=DE$ and $D\widehat{O}E=\theta$ . Show that $cos\theta =\frac{1}{4}$ .

   

3. The figure below shows a cyclic quadrilateral with $\frac{BC}{CD}=\frac{AD}{AB}$ .
   1. Show that the area of the cyclic quadrilateral is $DC·DA·sin\widehat{D}$ .
   2. Find expressions for $cos\widehat{D}$ and $cos\widehat{B}$ in terms of the quadrilateral sides.
   3. Show that $2C{A}^2=C{D}^2+D{A}^2+A{B}^2+B{C}^2$ .
   4. Suppose that $BC=10$ , $CD=15$ , $AD=4$ and $AB=6$ . Find $C{A}^2$ .
   5. Find the angle $\widehat{D}$ using your expression for $cos\widehat{D}$ . Hence find the area of $ABCD$ .

   

Problems in 3 dimensions

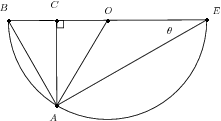
$D$ is the top of a tower of height $h$ . Its base is at $C$ . The triangle $ABC$ lies on the ground (a horizontal plane). If we have that $BC=b$ , $D\widehat{B}A=\alpha$ , $D\widehat{B}C=x$ and $D\widehat{C}B=\theta$ , show that

$$h=\frac{bsin\alpha sinx}{sin(x+\theta )}$$

1. Identify a strategy

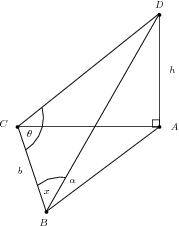
   We have that the triangle $ABD$ is right-angled. Thus we can relate the height $h$ with the angle $\alpha$ and either the length $BA$ or $BD$ (using sines or cosines). But we have two angles and a length for $▵BCD$ , and thus can work out all the remaining lengths and angles of this triangle. We can thus work out $BD$ .

2. Execute the strategy

   We have that

   $$\begin{array}{ccc}\hfill \frac{h}{BD}& =& sin\alpha \hfill \\ \hfill \Rightarrow h& =& BDsin\alpha \hfill \end{array}$$

   Now we need $BD$ in terms of the given angles and length $b$ . Considering the triangle $BCD$ , we see that we can use the sine rule.

   $$\begin{array}{ccc}\hfill \frac{sin\theta }{BD}& =& \frac{sin\left(B\widehat{D}C\right)}{b}\hfill \\ \hfill \Rightarrow BD& =& \frac{bsin\theta }{sin\left(b\widehat{D}C\right)}\hfill \end{array}$$

   But $D\widehat{B}C={180}^{\circ }-\alpha -\theta$ , and

   $$\begin{array}{ccc}\hfill sin({180}^{\circ }-\alpha -\theta )& =& -sin(-\alpha -\theta )\hfill \\ & =& sin(\alpha +\theta )\hfill \end{array}$$

   So

   $$\begin{array}{ccc}\hfill BD& =& \frac{bsin\theta }{sin\left(D\widehat{B}C\right)}\hfill \\ & =& \frac{bsin\theta }{sin(\alpha +\theta )}\hfill \end{array}$$

1. The line $BC$ represents a tall tower, with $C$ at its foot. Its angle of elevation from $D$ is $\theta$ . We are also given that $BA=AD=x$ .

   

   1. Find the height of the tower $BC$ in terms of $x$ , $tan\theta$ and $cos2\alpha$ .
   2. Find $BC$ if we are given that $x=140m$ , $\alpha ={21}^{\circ }$ and $\theta =9^{\circ }$ .

Other geometries

Taxicab geometry

Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the (absolute) differences of their coordinates.

Manhattan distance

The metric in taxi-cab geometry, is known as the Manhattan distance , between two points in an Euclidean space with fixed Cartesian coordinate system as the sum of the lengths of the projections of the line segment between the points onto the coordinate axes.

For example, the Manhattan distance between the point $P_1$ with coordinates $(x_1,y_1)$ and the point $P_2$ at $(x_2,y_2)$ is