1. Home
  2. Basic physics for medical imaging
  3. Radioactivity and nuclear physics
  4. Nuclear decay and conservation

7.4 Nuclear decay and conservation laws  (Page 4/25)

<< Chapter < Page
  Basic physics for medical imaging     Page 4 / 25
Chapter >> Page >

If a nuclide Z A X N is known to β − decay, then its β − decay equation is

Z A X N → Z + 1 A Y N − 1 + β − + ν - e ( β − decay ) , size 12{"" lSub { size 8{Z} } lSup { size 8{A} } X rSub { size 8{N} } rightarrow "" lSub { size 8{Z+1} } lSup { size 8{A} } Y rSub { size 8{N - 1} } +β rSup { size 8{ - {}} } + { bar {ν}} rSub { size 8{e} } ``` \( β rSup { size 8{ - {}} } `"decay" \) ,} {}

where Y is the nuclide having one more proton than X (see [link] ). So if you know that a certain nuclide β − decays, you can find the daughter nucleus by first looking up Z for the parent and then determining which element has atomic number Z + 1 . In the example of the β − decay of 60 Co size 12{"" lSup { size 8{"60"} } "Co"} {} given earlier, we see that Z = 27 for Co and Z = 28 is Ni. It is as if one of the neutrons in the parent nucleus decays into a proton, electron, and neutrino. In fact, neutrons outside of nuclei do just that—they live only an average of a few minutes and β − decay in the following manner:

n → p + β − + ν - e . size 12{n rightarrow p+β rSup { size 8{ - {}} } + { bar {ν}} rSub { size 8{e} } } {}
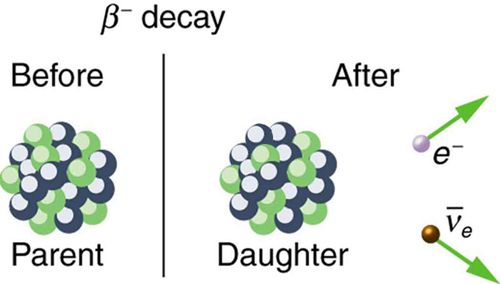
Image shows parent nucleus before beta decay and daughter nucleus after beta decay.
In β − size 12{β rSup { size 8{ - {}} } } {} decay, the parent nucleus emits an electron and an antineutrino. The daughter nucleus has one more proton and one less neutron than its parent. Neutrinos interact so weakly that they are almost never directly observed, but they play a fundamental role in particle physics.

We see that charge is conserved in β − decay, since the total charge is Z size 12{Z} {} before and after the decay. For example, in 60 Co decay, total charge is 27 before decay, since cobalt has Z = 27 . After decay, the daughter nucleus is Ni, which has Z = 28 , and there is an electron, so that the total charge is also 28 + (–1) or 27. Angular momentum is conserved, but not obviously (you have to examine the spins and angular momenta of the final products in detail to verify this). Linear momentum is also conserved, again imparting most of the decay energy to the electron and the antineutrino, since they are of low and zero mass, respectively. Another new conservation law is obeyed here and elsewhere in nature. The total number of nucleons A is conserved . In 60 Co decay, for example, there are 60 nucleons before and after the decay. Note that total A is also conserved in α decay. Also note that the total number of protons changes, as does the total number of neutrons, so that total Z size 12{Z} {} and total N size 12{N} {} are not conserved in β − size 12{β rSup { size 8{ - {}} } } {} decay, as they are in α size 12{α} {} decay. Energy released in β − size 12{β rSup { size 8{ - {}} } } {} decay can be calculated given the masses of the parent and products.

β − size 12{β rSup { size 8{ - {}} } } {} Decay energy from masses

Find the energy emitted in the β − size 12{β rSup { size 8{ - {}} } } {} decay of 60 Co size 12{"" lSup { size 8{"60"} } "Co"} {} .

Strategy and Concept

As in the preceding example, we must first find Δ m , the difference in mass between the parent nucleus and the products of the decay, using masses given in Appendix A . Then the emitted energy is calculated as before, using E = ( Δ m ) c 2 . The initial mass is just that of the parent nucleus, and the final mass is that of the daughter nucleus and the electron created in the decay. The neutrino is massless, or nearly so. However, since the masses given in Appendix A are for neutral atoms, the daughter nucleus has one more electron than the parent, and so the extra electron mass that corresponds to the β – is included in the atomic mass of Ni. Thus,

Δ m = m ( 60 Co ) − m ( 60 Ni ). size 12{Δm=m \( "" lSup { size 8{"60"} } "Co" \) -m \( "" lSup { size 8{"60"} } "Ni" \) } {}

Solution

The β − decay equation for 60 Co size 12{"" lSup { size 8{"60"} } "Co"} {} is

27 60 Co 33 → 28 60 Ni 32 + β − + ν ¯ e .

As noticed,

Δ m = m ( 60 Co ) − m ( 60 Ni ). size 12{Δm=m \( "" lSup { size 8{"60"} } "Co" \) -m \( "" lSup { size 8{"60"} } "Ni" \) } {}

Entering the masses found in Appendix A gives

Δ m = 59 . 933820 u − 59.930789 u = 0.003031 u .

Thus,

E = ( Δ m ) c 2 = ( 0.003031 u ) c 2 . size 12{E= \( Δm \) c rSup { size 8{2} } = \( 0 "." "003031" \) \( uc rSup { size 8{2} } \) } {}

Using 1 u = 931.5 MeV / c 2 , we obtain

E = ( 0 . 003031 ) ( 931.5 MeV / c 2 ) ( c 2 ) = 2 . 82 MeV. size 12{E= \( 0 "." "003031" \) \( "931" "." 5" MeV"/c rSup { size 8{2} } \) \( c rSup { size 8{2} } \) =2 "." "82"" MeV"} {}

Discussion and Implications

Perhaps the most difficult thing about this example is convincing yourself that the β − size 12{β rSup { size 8{ - {}} } } {} mass is included in the atomic mass of 60 Ni . Beyond that are other implications. Again the decay energy is in the MeV range. This energy is shared by all of the products of the decay. In many 60 Co decays, the daughter nucleus 60 Ni is left in an excited state and emits photons ( γ size 12{g} {} rays). Most of the remaining energy goes to the electron and neutrino, since the recoil kinetic energy of the daughter nucleus is small. One final note: the electron emitted in β − decay is created in the nucleus at the time of decay.

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>
Practice Key Terms 18

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Basic physics for medical imaging. OpenStax CNX. Feb 17, 2014 Download for free at http://legacy.cnx.org/content/col11630/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Basic physics for medical imaging' conversation and receive update notifications?

Ask