| << Chapter < Page | Chapter >> Page > |
The Poisson approximation to the binomial distribution
The following approximation is a classical one. We wish to show that for small p and sufficiently large n
Suppose with n large and . Then,
The first factor in the last expression is the ratio of polynomials in n of the same degree k , which must approach one as n becomes large. The second factor approaches one as n becomes large. According to a well known property of the exponential
The result is that for large n , , where .
The Poisson and gamma distributions
Suppose Poisson . Now gamma iff
A well known definite integral, obtained by integration by parts, is
Noting that we find after some simple algebra that
For and , we have the following equality iff gamma .
Now
The gaussian (normal) approximation
The central limit theorem, referred to in the discussion of the gaussian or normal distribution above, suggests that the binomial and Poisson distributions should be approximated by the gaussian.The number of successes in n trials has the binomial distribution. This random variable may be expressed
Since the mean value of X is and the variance is , the distribution should be approximately .
Use of the generating function shows that the sum of independent Poisson random variables is Poisson. Now if Poisson , then X may be considered the sum of n independent random variables, each Poisson . Since the mean value and the variance are both μ , it is reasonable to suppose that suppose that X is approximately .
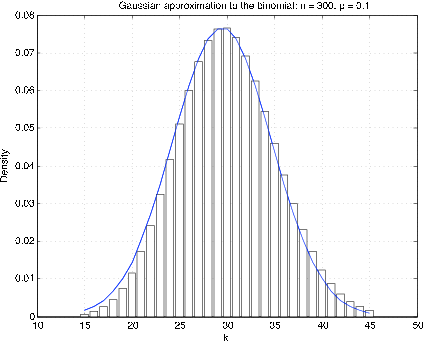
It is generally best to compare distribution functions. Since the binomial and Poisson distributions are integer-valued, it turns out that the best gaussian approximaton is obtainedby making a “continuity correction.” To get an approximation to a density for an integer-valued random variable, the probability at is represented by a rectangle of height p k and unit width, with k as the midpoint. Figure 1 shows a plot of the “density” and the corresponding gaussian density for , . It is apparent that the gaussian density is offset by approximately 1/2. To approximate the probability , take the area under the curve from ; this is called the continuity correction .

Notification Switch
Would you like to follow the 'Applied probability' conversation and receive update notifications?