| << Chapter < Page | Chapter >> Page > |
Use of m-procedures to compare
We have two m-procedures to make the comparisons. First, we consider approximation of the
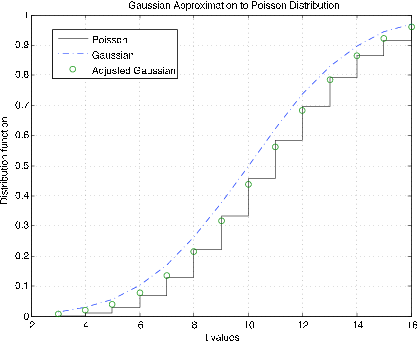
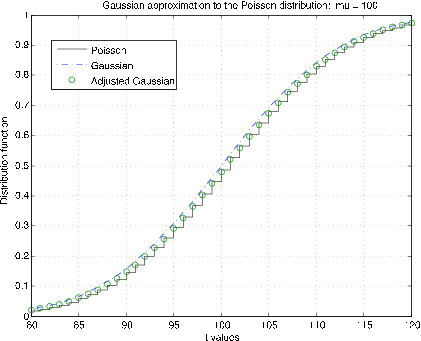
Poisson distribution. The m-procedure poissapp calls for a value of μ , selects a suitable range about and plots the distribution function for the Poisson distribution (stairs) and the normal (gaussian) distribution (dash dot) for . In addition, the continuity correction is applied to the gaussian distribution at integer values (circles). [link] shows plots for . It is clear that the continuity correction provides a much better approximation. The plots in [link] are for . Here the continuity correction provides the better approximation, but not by as much as for the smaller μ .

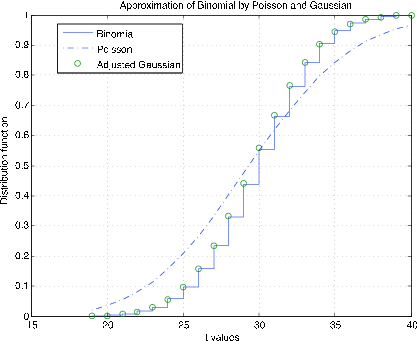
The m-procedure bincomp compares the binomial, gaussian, and Poisson distributions. It calls for values of n and p , selects suitable k values, and plots the distribution function for the binomial, a continuous approximation to the distribution function for the Poisson,and continuity adjusted values of the gaussian distribution function at the integer values. [link] shows plots for , . The good agreement of all three distribution functions is evident. [link] shows plots for , . There is still good agreement of the binomial and adjusted gaussian. However, the Poisson distribution does nottrack very well. The difficulty, as we see in the unit Variance , is the difference in variances— for the binomial as compared with for the Poisson.
Simple random variables play a significant role, both in theory and applications. In the unit Random Variables , we show how a simple random variable is determined by the set of points on the real line representingthe possible values and the corresponding set of probabilities that each of these values is taken on. This describes the distribution of the random variable and makes possible calculations of eventprobabilities and parameters for the distribution.
A continuous random variable is characterized by a set of possible values spread continuously over an interval or collection of intervals. In this case, the probability is also spread smoothly. The distributionis described by a probability density function, whose value at any point indicates "the probability per unit length" near the point. A simple approximation is obtained by subdividing an interval whichincludes the range (the set of possible values) into small enough subintervals that the density is approximately constant over each subinterval. A point in each subinterval is selected and is assigned the probabilitymass in its subinterval. The combination of the selected points and the corresponding probabilities describes the distribution of an approximating simple random variable. Calculations based on thisdistribution approximate corresponding calculations on the continuous distribution.

Notification Switch
Would you like to follow the 'Applied probability' conversation and receive update notifications?