6.2 Discovery of the parts of the atom: electrons and nuclei  (Page 5/7)

Although the results of the experiment were published by his colleagues in 1909, it took Rutherford two years to convince himself of their meaning. Like Thomson before him, Rutherford was reluctant to accept such radical results. Nature on a small scale is so unlike our classical world that even those at the forefront of discovery are sometimes surprised. Rutherford later wrote: “It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you. On consideration, I realized that this scattering backwards ... [meant] ... the greatest part of the mass of the atom was concentrated in a tiny nucleus.” In 1911, Rutherford published his analysis together with a proposed model of the atom. The size of the nucleus was determined to be about ${\text{10}}^{-\text{15}}\text{m}$ , or 100,000 times smaller than the atom. This implies a huge density, on the order of ${\text{10}}^{\text{15}}{\text{g/cm}}^3$ , vastly unlike any macroscopic matter. Also implied is the existence of previously unknown nuclear forces to counteract the huge repulsive Coulomb forces among the positive charges in the nucleus. Huge forces would also be consistent with the large energies emitted in nuclear radiation.

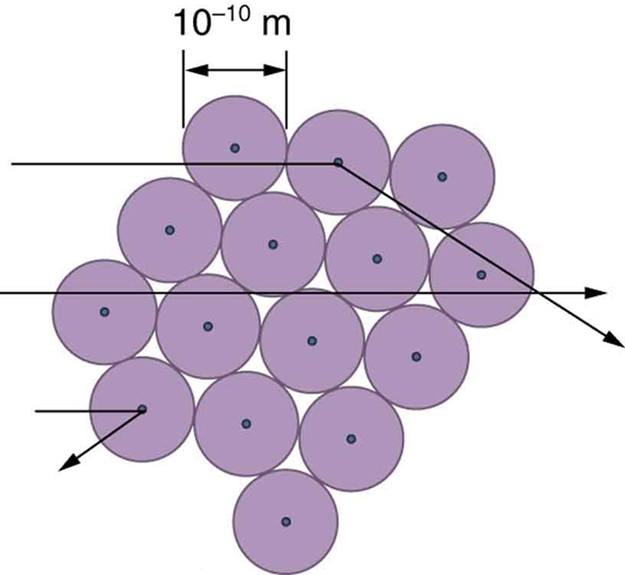
The small size of the nucleus also implies that the atom is mostly empty inside. In fact, in Rutherford’s experiment, most alphas went straight through the gold foil with very little scattering, since electrons have such small masses and since the atom was mostly empty with nothing for the alpha to hit. There were already hints of this at the time Rutherford performed his experiments, since energetic electrons had been observed to penetrate thin foils more easily than expected. [link] shows a schematic of the atoms in a thin foil with circles representing the size of the atoms (about ${\text{10}}^{-\text{10}}\text{m}$ ) and dots representing the nuclei. (The dots are not to scale—if they were, you would need a microscope to see them.) Most alpha particles miss the small nuclei and are only slightly scattered by electrons. Occasionally, (about once in 8000 times in Rutherford’s experiment), an alpha hits a nucleus head-on and is scattered straight backward.

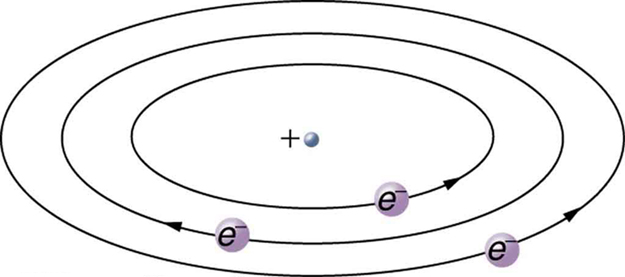
Based on the size and mass of the nucleus revealed by his experiment, as well as the mass of electrons, Rutherford proposed the planetary model of the atom    . The planetary model of the atom pictures low-mass electrons orbiting a large-mass nucleus. The sizes of the electron orbits are large compared with the size of the nucleus, with mostly vacuum inside the atom. This picture is analogous to how low-mass planets in our solar system orbit the large-mass Sun at distances large compared with the size of the sun. In the atom, the attractive Coulomb force is analogous to gravitation in the planetary system. (See [link] .) Note that a model or mental picture is needed to explain experimental results, since the atom is too small to be directly observed with visible light.

Rutherford’s planetary model of the atom was crucial to understanding the characteristics of atoms, and their interactions and energies, as we shall see in the next few sections. Also, it was an indication of how different nature is from the familiar classical world on the small, quantum mechanical scale. The discovery of a substructure to all matter in the form of atoms and molecules was now being taken a step further to reveal a substructure of atoms that was simpler than the 92 elements then known. We have continued to search for deeper substructures, such as those inside the nucleus, with some success. In later chapters, we will follow this quest in the discussion of quarks and other elementary particles, and we will look at the direction the search seems now to be heading.

Phet explorations: rutherford scattering

How did Rutherford figure out the structure of the atom without being able to see it? Simulate the famous experiment in which he disproved the Plum Pudding model of the atom by observing alpha particles bouncing off atoms and determining that they must have a small core.

Section summary

• Atoms are composed of negatively charged electrons, first proved to exist in cathode-ray-tube experiments, and a positively charged nucleus.
• All electrons are identical and have a charge-to-mass ratio of
  $\frac{q_e}{m_e}=-\text{1.76}\times {\text{10}}^{\text{11}}\text{C/kg.}$
• The positive charge in the nuclei is carried by particles called protons, which have a charge-to-mass ratio of
  $\frac{q_p}{m_p}=9\text{.}\text{57}\times {\text{10}}^7\text{C/kg}\text{.}$
• Mass of electron,
  $m_e=9\text{.}\text{11}\times {\text{10}}^{-\text{31}}\text{kg}\text{.}$
• Mass of proton,
  $m_p=1\text{.}\text{67}\times {\text{10}}^{-\text{27}}\text{kg.}$
• The planetary model of the atom pictures electrons orbiting the nucleus in the same way that planets orbit the sun.

Conceptual questions

Problem exercises