| << Chapter < Page | Chapter >> Page > |
Die maatstawwe van sentrale neiging (gemiddelde, mediaan, modus) en die bepalers van verspreiding (reeks, semi-inter-kwartielreeks, kwartiele, persentiele, inter-kwartielreeks) is numeriese metodes om data op te som. Hierdie afdeling bied metodes wat die opgesomde data met behulp van grafieke voorstel.
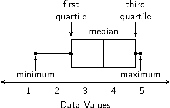
Een metode om data voor te stel is met behulp van 'n vyf-getal opsomming . Die vyf getalle is: minimum, eerste kwartiel, mediaan, derde kwartiel en maksimum.
'n Houer-en-puntdiagram is 'n metode om die vyf-getal opsomming grafies voor te stel.
Die hoof eienskappe van 'n houer-en-puntdiagram word getoon in [link] . Die boks kan horisontaal lê (soos aangedui) of vertikaal. Vir 'n horisontale diagram, is die linkerkant van die boks geplaas by die eerste kwartiel en die regter kant van die boks is geplaas op die derde kwartiel. Die hoogte van die boks is arbitrêr, want daar is geen -as. Binne-in die boks word die maatstawwe van sentrale neiging aangedui. Die mediaan word getoon met 'n vertikale lyn wat die boks in twee deel. Die gemiddeld word as 'n sterretjie aangeduien die minimum en maksimum waardes word met reguit lyne verbind aan die houer.

Teken 'n houer-en-puntdiagram vir die datastel
.
Minimum = 1,25
Maksimum = 5,10
Posisie van eerste kwartiel = tuessen 3 en 4
Posisie van tweede kwartiel = tussen 6 en 7
Posisie van derde kwartiel = tussen 9 en 10
Data punt tussen 3 en 4 =
Data punt tussen between 6 en 7 =
Data punt tussen between 9 en 10 =
Die vyf-getal opsomming is dus: 1,25; 2,5; 3,65; 4,775; 5,10.
Khan academy video oor houer-en-puntdiagramme
Kumulatiewe histogramme, ook bekend as ogiewe, is 'n plot van kumulatiewe frekwensies en word gebruik om te bepaal hoeveel data waardes lê bo of onder 'n spesifieke waarde in 'n datastel. Die kumulatiewe frekwensie word bereken vanaf 'n frekwensie-tabel, deur die toevoeging van elke frekwensie van die totale van die frekwensies van al die data waardes voor dit in die datastel. Die laaste waarde vir die kumulatiewe frekwensie sal altyd gelyk wees aan die totale getal van data waardes, aangesien alle frekwensies reeds na die vorige totaal bygevoeg. Die kumulatiewe frekwensie is geplot by die boonste grens van die interval.
Die kumulatiewe frekwensies van Data Stel 2 word as in voorbeeld vertoon in [link] en grafies voorgestel in [link] .
| Intervalle | ||||||
| Frekwensie | 30 | 32 | 35 | 34 | 37 | 32 |
| Kumulatiewe Frekwensies | 30 | 30 + 32 | 30 + 32 + 35 | 30 + 32 + 35 + 34 | 30 + 32 + 35 + 34 + 37 | 30 + 32 + 35 + 34 + 37 + 32 |
| 30 | 62 | 97 | 131 | 168 | 200 |
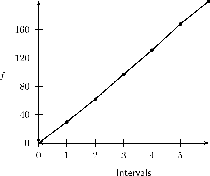
Let op dat die frekwensies by die boonste limiet van die interval geplot word. Die punte (30;1) (62;2) (97;3) is dus geplot. Dit verskil van die frekwensieveelhoek waar ons frekwensies by die middelpunte van die intervalle plot.

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 11)' conversation and receive update notifications?