5.2 Infinite series  (Page 9/16)

[T] Find the probability that a fair coin is flipped a multiple of three times before coming up heads.

[T] Find the probability that a fair coin will come up heads for the second time after an even number of flips.

[T] Find a series that expresses the probability that a fair coin will come up heads for the second time on a multiple of three flips.

[T] The expected number of times that a fair coin will come up heads is defined as the sum over $n=1,2\text{,…}$ of $n$ times the probability that the coin will come up heads exactly $n$ times in a row, or $n\text{/}{2}^{n+1}.$ Compute the expected number of consecutive times that a fair coin will come up heads.

[T] A person deposits $\text{\$}10$ at the beginning of each quarter into a bank account that earns $4\text{\%}$ annual interest compounded quarterly (four times a year).

1. Show that the interest accumulated after $n$ quarters is $\text{\$}10\left(\frac{{1.01}^{n+1}-1}{0.01}-n\right).$
2. Find the first eight terms of the sequence.
3. How much interest has accumulated after $2$ years?

[T] Suppose that the amount of a drug in a patient’s system diminishes by a multiplicative factor $r<1$ each hour. Suppose that a new dose is administered every $N$ hours. Find an expression that gives the amount $A\left(n\right)$ in the patient’s system after $n$ hours for each $n$ in terms of the dosage $d$ and the ratio $r.$ ( Hint: Write $n=mN+k,$ where $0\le k<N,$ and sum over values from the different doses administered.)

[T] A certain drug is effective for an average patient only if there is at least $1$ mg per kg in the patient’s system, while it is safe only if there is at most $2$ mg per kg in an average patient’s system. Suppose that the amount in a patient’s system diminishes by a multiplicative factor of $0.9$ each hour after a dose is administered. Find the maximum interval $N$ of hours between doses, and corresponding dose range $d$ (in mg/kg) for this $N$ that will enable use of the drug to be both safe and effective in the long term.

Suppose that $a_n\ge 0$ is a sequence of numbers. Explain why the sequence of partial sums of $a_n$ is increasing.

[T] Suppose that $a_n$ is a sequence of positive numbers and the sequence $S_n$ of partial sums of $a_n$ is bounded above. Explain why ${\displaystyle \sum _{n=1}^{\infty }{a}_n}$ converges. Does the conclusion remain true if we remove the hypothesis $a_n\ge 0\text{?}$

[T] Suppose that $a_1=S_1=1$ and that, for given numbers $S>1$ and $0<k<1,$ one defines $a_{n+1}=k(S-S_n)$ and $S_{n+1}=a_{n+1}+S_n.$ Does $S_n$ converge? If so, to what? ( Hint: First argue that $S_n<S$ for all $n$ and $S_n$ is increasing.)

[T] A version of von Bertalanffy growth can be used to estimate the age of an individual in a homogeneous species from its length if the annual increase in year $n+1$ satisfies $a_{n+1}=k(S-S_n),$ with $S_n$ as the length at year $n,$ $S$ as a limiting length, and $k$ as a relative growth constant. If $S_1=3,$ $S=9,$ and $k=1\text{/}2,$ numerically estimate the smallest value of $n$ such that $S_n\ge 8.$ Note that $S_{n+1}=S_n+a_{n+1}.$ Find the corresponding $n$ when $k=1\text{/}4.$

[T] Suppose that ${\displaystyle \sum _{n=1}^{\infty }{a}_n}$ is a convergent series of positive terms. Explain why $\underset{N\to \infty }{\text{lim}}{\displaystyle \sum _{n=N+1}^{\infty }{a}_n=0}.$

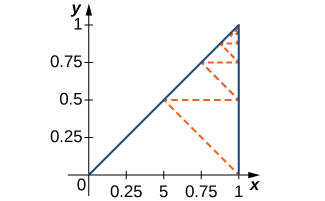
[T] Find the length of the dashed zig-zag path in the following figure.

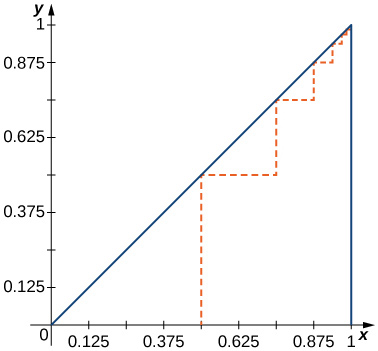
[T] Find the total length of the dashed path in the following figure.

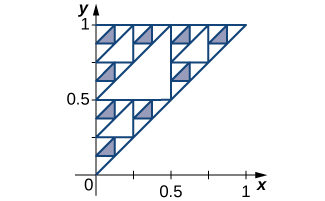
[T] The Sierpinski triangle is obtained from a triangle by deleting the middle fourth as indicated in the first step, by deleting the middle fourths of the remaining three congruent triangles in the second step, and in general deleting the middle fourths of the remaining triangles in each successive step. Assuming that the original triangle is shown in the figure, find the areas of the remaining parts of the original triangle after $N$ steps and find the total length of all of the boundary triangles after $N$ steps.

[T] The Sierpinski gasket is obtained by dividing the unit square into nine equal sub-squares, removing the middle square, then doing the same at each stage to the remaining sub-squares. The figure shows the remaining set after four iterations. Compute the total area removed after $N$ stages, and compute the length the total perimeter of the remaining set after $N$ stages.