5.2 Infinite series  (Page 8/16)

${\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^{13}}}-\frac{1}{{\left(n+1\right)}^{13}}$

${\displaystyle \sum _{n=1}^{\infty }\left(\sqrt{n}-\sqrt{n+1}\right)}$

${\displaystyle \sum _{n=1}^{\infty }\left(\text{sin}n-\text{sin}\left(n+1\right)\right)}$

${\displaystyle \sum _{n=1}^{\infty }\text{ln}\left(\frac{n}{n+1}\right)}$

${\displaystyle \sum _{n=1}^{\infty }\frac{2n+1}{{\left(n^2+n\right)}^2}}$ ( Hint: Factor denominator and use partial fractions.)

${\displaystyle \sum _{n=2}^{\infty }\frac{\text{ln}\left(1{+}_n^1\right)}{\text{ln}n\text{ln}\left(n+1\right)}}$

${\displaystyle \sum _{n=1}^{\infty }\frac{\left(n+2\right)}{n\left(n+1\right)2^{n+1}}}$ ( Hint: Look at $1\text{/}\left(n{2}^n\right).)$

Let $a_n=f\left(n\right)-2f\left(n+1\right)+f\left(n+2\right),$ in which $f\left(n\right)\to 0$ as $n\to \infty .$ Find ${\displaystyle \sum _{n=1}^{\infty }{a}_n}.$

$a_n=f\left(n\right)-f\left(n+1\right)-f\left(n+2\right)+f\left(n+3\right),$ in which $f\left(n\right)\to 0$ as $n\to \infty .$ Find ${\displaystyle \sum _{n=1}^{\infty }{a}_n}.$

Suppose that $a_n=c_{0}f\left(n\right)+c_{1}f\left(n+1\right)+c_{2}f\left(n+2\right)+c_{3}f\left(n+3\right)+c_{4}f\left(n+4\right),$ where $f\left(n\right)\to 0$ as $n\to \infty .$ Find a condition on the coefficients $c_0\text{,…},c_4$ that make this a general telescoping series.

Evaluate ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{n\left(n+1\right)\left(n+2\right)}}$ ( Hint: $\frac{1}{n\left(n+1\right)\left(n+2\right)}=\frac{1}{2n}-\frac{1}{n+1}+\frac{1}{2\left(n+2\right)})$

Evaluate ${\displaystyle \sum _{n=2}^{\infty }\frac{2}{n^3-n}}.$

Find a formula for ${\displaystyle \sum _{n=1}^{\infty }\frac{1}{n\left(n+N\right)}}$ where $N$ is a positive integer.

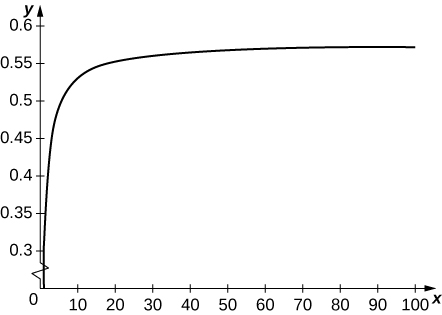
[T] Define a sequence $t_k={\displaystyle \sum _{n=1}^{k-1}(1\text{/}k)-\text{ln}k.}$ Use the graph of $1\text{/}x$ to verify that $t_k$ is increasing. Plot $t_k$ for $k=1\text{…}100$ and state whether it appears that the sequence converges.

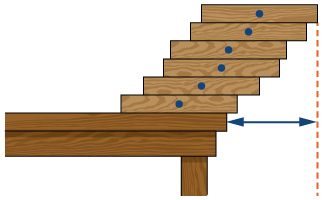
[T] Suppose that $N$ equal uniform rectangular blocks are stacked one on top of the other, allowing for some overhang. Archimedes’ law of the lever implies that the stack of $N$ blocks is stable as long as the center of mass of the top $\left(N-1\right)$ blocks lies at the edge of the bottom block. Let $x$ denote the position of the edge of the bottom block, and think of its position as relative to the center of the next-to-bottom block. This implies that $(N-1)x=\left(\frac{1}{2}-x\right)$ or $x=1\text{/}\left(2N\right).$ Use this expression to compute the maximum overhang (the position of the edge of the top block over the edge of the bottom block.) See the following figure.

[T] $\pi =\mathrm{-3}+{\displaystyle \sum _{n=1}^{\infty }\frac{n{2}^{n}n{\text{!}}^2}{\left(2n\right)\text{!}}},$ error $<0.0001$

[T] $\frac{\pi }{2}={\displaystyle \sum _{k=0}^{\infty }\frac{k\text{!}}{\left(2k+1\right)\text{!}\text{!}}}={\displaystyle \sum _{k=0}^{\infty }\frac{2^{k}k{\text{!}}^2}{\left(2k+1\right)\text{!}}},$ error $<{10}^{\mathrm{-4}}$

[T] $\frac{9801}{2\pi }=\frac{4}{9801}{\displaystyle \sum _{k=0}^{\infty }\frac{\left(4k\right)\text{!}\left(1103+26390k\right)}{{\left(k\text{!}\right)}^4{396}^{4k}}},$ error $<{10}^{\mathrm{-12}}$

[T] $\frac{1}{12\pi }={\displaystyle \sum _{k=0}^{\infty }\frac{{\left(\mathrm{-1}\right)}^k\left(6k\right)\text{!}\left(13591409+545140134k\right)}{\left(3k\right)\text{!}{\left(k\text{!}\right)}^3{640320}^{3k+3\text{/}2}}},$ error $<{10}^{\mathrm{-15}}$

[T] A fair coin is one that has probability $1\text{/}2$ of coming up heads when flipped.

1. What is the probability that a fair coin will come up tails $n$ times in a row?
2. Find the probability that a coin comes up heads for the first time after an even number of coin flips.