| << Chapter < Page | Chapter >> Page > |
From we see that . Substituting this into the expression for gives
We write this relationship in two different ways and gain two different insights:
The first relationship in states that the linear velocity is proportional to the distance from the center of rotation, thus, it is largest for a point on the rim (largest ), as you might expect. We can also call this linear speed of a point on the rim the tangential speed . The second relationship in can be illustrated by considering the tire of a moving car. Note that the speed of a point on the rim of the tire is the same as the speed of the car. See [link] . So the faster the car moves, the faster the tire spins—large means a large , because . Similarly, a larger-radius tire rotating at the same angular velocity ( ) will produce a greater linear speed ( ) for the car.
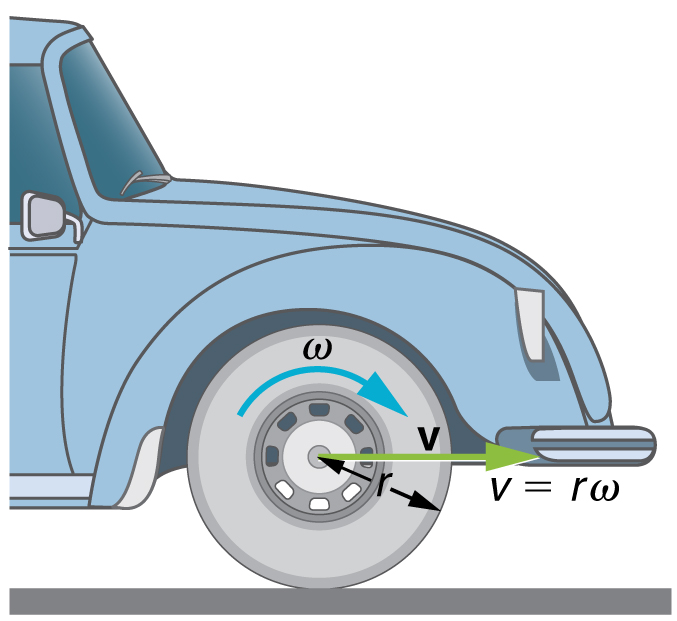
Calculate the angular velocity of a 0.300 m radius car tire when the car travels at (about ). See [link] .
Strategy
Because the linear speed of the tire rim is the same as the speed of the car, we have The radius of the tire is given to be Knowing and , we can use the second relationship in to calculate the angular velocity.
Solution
To calculate the angular velocity, we will use the following relationship:
Substituting the knowns,
Discussion
When we cancel units in the above calculation, we get 50.0/s. But the angular velocity must have units of rad/s. Because radians are actually unitless (radians are defined as a ratio of distance), we can simply insert them into the answer for the angular velocity. Also note that if an earth mover with much larger tires, say 1.20 m in radius, were moving at the same speed of 15.0 m/s, its tires would rotate more slowly. They would have an angular velocity
Both and have directions (hence they are angular and linear velocities , respectively). Angular velocity has only two directions with respect to the axis of rotation—it is either clockwise or counterclockwise. Linear velocity is tangent to the path, as illustrated in [link] .
Tie an object to the end of a string and swing it around in a horizontal circle above your head (swing at your wrist). Maintain uniform speed as the object swings and measure the angular velocity of the motion. What is the approximate speed of the object? Identify a point close to your hand and take appropriate measurements to calculate the linear speed at this point. Identify other circular motions and measure their angular velocities.

Notification Switch
Would you like to follow the 'Physics 101' conversation and receive update notifications?