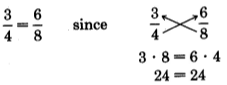This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses proportions. By the end of the module students should be able to describe proportions and find the missing factor in a proportion and be able to work with proportions involving rates.
Section overview
- Ratios, Rates, and Proportions
- Finding the Missing Factor in a Proportion
- Proportions Involving Rates
Ratios, rates, and proportions
Ratio, rate
We have defined a
ratio as a comparison, by division, of two pure numbers or two
like denominate numbers. We have defined a
rate as a comparison, by division, of two
unlike denominate numbers.
Proportion
A
proportion is a statement that two ratios or rates are equal. The following two examples show how to read proportions.

Sample set a
Write or read each proportion.
3 is to 5 as 12 is to 20
10 items is to 5 dollars as 2 items is to 1 dollar
8 is to 12 as 16 is to 24.
50 milligrams of vitamin C is to 1 tablet as 300 milligrams of vitamin C is to 6 tablets.
Practice set a
Write or read each proportion.
2 people are to 1 window as 10 people are to 5 windows
15 is to 4 as 75 is to 20.
2 plates are to 1 tray as 20 plates are to 10 trays.
Finding the missing factor in a proportion
Many practical problems can be solved by writing the given information as proportions. Such proportions will be composed of three specified numbers and one unknown number. It is customary to let a letter, such as
, represent the unknown number. An example of such a proportion is
This proportion is read as "
is to 4 as 20 is to 16."
There is a method of solving these proportions that is based on the equality of fractions. Recall that two fractions are equivalent if and only if their cross products are equal. For example,
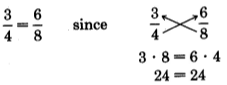
Notice that in a proportion that contains three specified numbers and a letter representing an unknown quantity, that regardless of where the letter appears, the following situation always occurs.
We recognize this as a multiplication statement. Specifically, it is a missing factor statement. (See
[link] for a discussion of multiplication statements.) For example,
Each of these statements is a multiplication statement. Specifically, each is a missing factor statement. (The letter used here is
, whereas
was used in
[link] .)
Finding the missing factor in a proportion
The missing factor in a missing factor statement can be determined by dividing the product by the known factor, that is, if
represents the missing factor, then
Sample set b
Find the unknown number in each proportion.
. Find the cross product.
This mean that
, or 5 is to 4 as 20 is to 16.