4.8 Elasticity: stress and strain  (Page 9/15)

A 20.0-m tall hollow aluminum flagpole is equivalent in strength to a solid cylinder 4.00 cm in diameter. A strong wind bends the pole much as a horizontal force of 900 N exerted at the top would. How far to the side does the top of the pole flex?

As an oil well is drilled, each new section of drill pipe supports its own weight and that of the pipe and drill bit beneath it. Calculate the stretch in a new 6.00 m length of steel pipe that supports 3.00 km of pipe having a mass of 20.0 kg/m and a 100-kg drill bit. The pipe is equivalent in strength to a solid cylinder 5.00 cm in diameter.

Calculate the force a piano tuner applies to stretch a steel piano wire 8.00 mm, if the wire is originally 0.850 mm in diameter and 1.35 m long.

A vertebra is subjected to a shearing force of 500 N. Find the shear deformation, taking the vertebra to be a cylinder 3.00 cm high and 4.00 cm in diameter.

A disk between vertebrae in the spine is subjected to a shearing force of 600 N. Find its shear deformation, taking it to have the shear modulus of $1\times {\text{10}}^9\text{N}/{\text{m}}^2$ . The disk is equivalent to a solid cylinder 0.700 cm high and 4.00 cm in diameter.

When using a pencil eraser, you exert a vertical force of 6.00 N at a distance of 2.00 cm from the hardwood-eraser joint. The pencil is 6.00 mm in diameter and is held at an angle of $\text{20.0º}$ to the horizontal. (a) By how much does the wood flex perpendicular to its length? (b) How much is it compressed lengthwise?

To consider the effect of wires hung on poles, we take data from [link] , in which tensions in wires supporting a traffic light were calculated. The left wire made an angle $\text{30.0º}$ below the horizontal with the top of its pole and carried a tension of 108 N. The 12.0 m tall hollow aluminum pole is equivalent in strength to a 4.50 cm diameter solid cylinder. (a) How far is it bent to the side? (b) By how much is it compressed?

A farmer making grape juice fills a glass bottle to the brim and caps it tightly. The juice expands more than the glass when it warms up, in such a way that the volume increases by 0.2% (that is, $\mathrm{\Delta }V/V_0=2\times {\text{10}}^{-3}$ ) relative to the space available. Calculate the force exerted by the juice per square centimeter if its bulk modulus is $1\text{.}8\times {\text{10}}^9{\text{N/m}}^2$ , assuming the bottle does not break. In view of your answer, do you think the bottle will survive?

(a) When water freezes, its volume increases by 9.05% (that is, $\mathrm{\Delta }V/V_0=9\text{.}\text{05}\times {\text{10}}^{-2}$ ). What force per unit area is water capable of exerting on a container when it freezes? (It is acceptable to use the bulk modulus of water in this problem.) (b) Is it surprising that such forces can fracture engine blocks, boulders, and the like?

This problem returns to the tightrope walker studied in [link] , who created a tension of $3\text{.}\text{94}\times {\text{10}}^3\mathrm{N}$ in a wire making an angle $\text{5.0º}$ below the horizontal with each supporting pole. Calculate how much this tension stretches the steel wire if it was originally 15 m long and 0.50 cm in diameter.

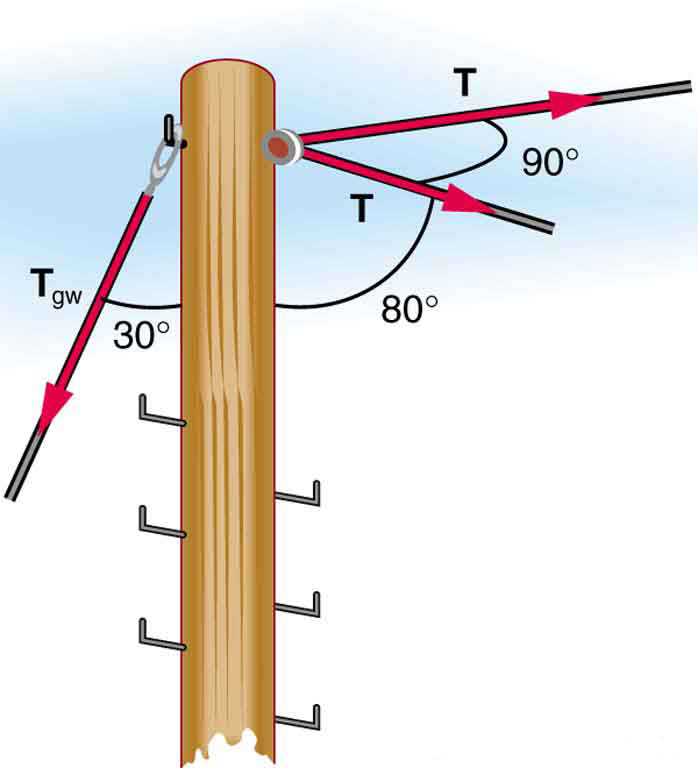
The pole in [link] is at a $\text{90.0º}$ bend in a power line and is therefore subjected to more shear force than poles in straight parts of the line. The tension in each line is $4\text{.}\text{00}\times {\text{10}}^4\mathrm{N}$ , at the angles shown. The pole is 15.0 m tall, has an 18.0 cm diameter, and can be considered to have half the strength of hardwood. (a) Calculate the compression of the pole. (b) Find how much it bends and in what direction. (c) Find the tension in a guy wire used to keep the pole straight if it is attached to the top of the pole at an angle of $\text{30.0º}$ with the vertical. (Clearly, the guy wire must be in the opposite direction of the bend.)