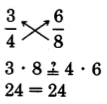This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module reviews the key concepts from the chapter "Introduction to Fractions and Multiplication and Division of Fractions."
Summary of key concepts
Fraction (
[link] )
The idea of breaking up a whole quantity into equal parts gives us the word
fraction .
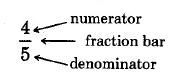
Fraction bar, denominator, numerator (
[link] )
A fraction has three parts:
- The fraction bar
- The nonzero whole number below the fraction bar is the
denominator .
- The whole number above the fraction bar is the
numerator .
Proper fraction (
[link] )
Proper fractions are fractions in which the numerator is strictly less than the denominator.
is a proper fraction
Improper fraction (
[link] )
Improper fractions are fractions in which the numerator is greater than or equal to the denominator. Also, any nonzero number placed over 1 is an improper fraction.
,
, and
are improper fractions
Mixed number (
[link] )
A
mixed number is a number that is the sum of a whole number and a proper fraction.
is a mixed number
Correspondence between improper fractions and mixed numbers (
[link] )
Each improper fraction corresponds to a particular mixed number, and each mixed number corresponds to a particular improper fraction.
Converting an improper fraction to a mixed number (
[link] )
A method, based on division, converts an improper fraction to an equivalent mixed number.
can be converted to
Converting a mixed number to an improper fraction (
[link] )
A method, based on multiplication, converts a mixed number to an equivalent improper fraction.
can be converted to
Equivalent fractions (
[link] )
Fractions that represent the same quantity are
equivalent fractions .
and
are equivalent fractions
Test for equivalent fractions (
[link] )
If the
cross products of two fractions are equal, then the two fractions are equivalent.
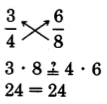
Thus,
and
are equivalent.
Relatively prime (
[link] )
Two whole numbers are
relatively prime when 1 is the only number that divides both of them.
3 and 4 are relatively prime
Reduced to lowest terms (
[link] )
A fraction is
reduced to lowest terms if its numerator and denominator are relatively prime.
The number
is reduced to lowest terms, since 3 and 4 are relatively prime.
The number
is
not reduced to lowest terms since 6 and 8 are not relatively prime.
Reducing fractions to lowest terms (
[link] )
Two methods, one based on dividing out common primes and one based on dividing out any common factors, are available for reducing a fraction to lowest terms.
Raising fractions to higher terms (
[link] )
A fraction can be raised to higher terms by multiplying both the numerator and denominator by the same nonzero number.
The word “of” means multiplication (
[link] )
In many mathematical applications, the word "of" means multiplication.
Multiplication of fractions (
[link] )
To multiply two or more fractions, multiply the numerators together and multiply the denominators together. Reduce if possible.
Multiplying fractions by dividing out common factors (
[link] )
Two or more fractions can be multiplied by first dividing out common factors and then using the rule for multiplying fractions.
Multiplication of mixed numbers (
[link] )
To perform a multiplication in which there are mixed numbers, first convert each mixed number to an improper fraction, then multiply. This idea also applies to division of mixed numbers.
Reciprocals (
[link] )
Two numbers whose product is 1 are reciprocals.
7 and
are reciprocals
Division of fractions (
[link] )
To divide one fraction by another fraction, multiply the dividend by the reciprocal of the divisor.
Dividing 1 by a fraction (
[link] )
When dividing 1 by a fraction, the quotient is the reciprocal of the fraction.
Multiplication statements (
[link] )
A mathematical statement of the form
product = (factor 1) (factor 2)
is a multiplication statement.
By omitting one of the three numbers, one of three following problems result:
-
M = (factor 1) ⋅ (factor 2) Missing product statement.
- product = (factor 1) ⋅
M Missing factor statement.
- product =
M ⋅ (factor 2) Missing factor statement.
Missing products are determined by simply multiplying the known factors.
Missing factors are determined by
missing factor = (product) ÷ (known factor)