Digital convolution has serveral characteristics, allowing different system connection configurations.
Commutativity
By a change of variable
n
−
k
=
k
,
size 12{n - k=k rSup { size 8{,} } } {} , or
k
=
n
−
k
,
size 12{k=n - k rSup { size 8{,} } } {} in the formula for convolution
y
(
n
)
=
∑
k
=
−
∞
∞
x
(
k
)
h
(
n
−
k
)
=
∑
k
,
=
−
∞
∞
x
(
n
−
k
,
)
h
(
k
,
)
size 12{y \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {x \( k \) h \( n - k \) } = Sum cSub { size 8{k rSup { size 6{,} } = - infinity } } cSup { infinity } {x \( n - k rSup { size 8{,} } \) h \( k rSup { size 8{,} } \) } } {}
Example
and by replacing the temporary variable k’ by k, we get
y
(
n
)
=
∑
k
=
−
∞
∞
x
(
n
−
k
)
h
(
k
)
=
∑
k
=
−
∞
∞
h
(
k
)
x
(
n
−
k
)
=
h
(
k
)
∗
x
(
k
−
n
)
size 12{y \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {x \( n - k \) h \( k \) } = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {h \( k \) x \( n - k \) =h \( k \) *x \( k - n \) } } {}
That is the order of convolution is reversed. Thus we have two formulae of convolution:
y
(
n
)
=
x
(
n
)
∗
h
(
n
)
=
∑
k
=
−
∞
∞
x
(
k
)
h
(
n
−
k
)
size 12{y \( n \) =x \( n \) * h \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {x \( k \) h \( n - k \) } } {}
and
y
(
n
)
=
h
(
n
)
∗
x
(
n
)
=
∑
k
=
−
∞
∞
h
(
k
)
x
(
n
−
k
)
size 12{y \( n \) =h \( n \) * x \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {h \( k \) x \( n - k \) } } {}
In practive we usually let the longer sequence stay fixed, and shift the shorter one.
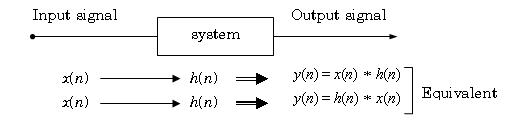
The commutative characteristic of convolution means that we can swap the input signal with the impulse response of a system without affecting the output. This idea is depicted in
[link] .
Commutation between input signal and impluse response gives the same output
Associativity
It can be shown that
[
x
(
n
)
∗
h
1
(
n
)
]
∗
h
2
(
n
)
=
x
(
n
)
∗
[
h
1
(
n
)
∗
h
2
(
n
)
]
size 12{ \[ x \( n \) *h rSub { size 8{1} } \( n \) \] *h rSub { size 8{2} } \( n \) =x \( n \) * \[ h rSub { size 8{1} } \( n \) *h rSub { size 8{2} } \( n \) \]} {}
[link] shows the system meaning of the associativity, where two systems in series (in cascade) can be replaced by only one whose impulse response is the convolution of the two individual impulse responses.
Impluse response of two systems in cascade
Two systems in cascade have impulse responses
h
1
(
n
)
=
a
n
u
(
n
)
h
2
(
n
)
=
b
n
u
(
n
)
alignl { stack {
size 12{h rSub { size 8{1} } \( n \) =a rSup { size 8{n} } u \( n \) } {} #h rSub { size 8{2} } \( n \) =b rSup { size 8{n} } u \( n \) {}
} } {} Find the overall impulse response.
Solution
First
∣
a
∣
size 12{ lline a rline } {} and
∣
b
∣
size 12{ lline b rline } {} should be smaller than 1 to ensure the convergence of the sequences. Notice that both impulse responses are causal. The overall impulse response is
h
(
n
)
=
h
1
(
n
)
∗
h
2
(
n
)
=
∑
k
=
−
∞
∞
h
1
(
k
)
h
2
(
n
−
k
)
size 12{h \( n \) =h rSub { size 8{1} } \( n \) * h rSub { size 8{2} } \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {h rSub { size 8{1} } \( k \) h rSub { size 8{2} } \( n - k \) } } {}
The actual limits of summation are
k
=
0
size 12{k=0} {} and
k
=
n
size 12{k=n} {} (see
[link] later), hence
h
(
n
)
=
∑
k
=
0
n
a
k
b
k
−
n
u
(
k
)
u
(
k
−
n
)
=
b
n
∑
k
=
0
n
(
a
b
)
k
alignl { stack {
size 12{h \( n \) = Sum cSub { size 8{k=0} } cSup { size 8{n} } {a rSup { size 8{k} } b rSup { size 8{k - n} } u \( k \) u \( k - n \) } } {} #matrix {
{} # {} # {}} =b rSub { size 8{n} } Sum cSub { size 8{k=0} } cSup { size 8{n} } { \( { { size 8{a} } over { size 8{b} } } \) rSup { size 8{k} } } {}
} } {}
Using the formula of finite geometric series.
1
+
x
+
x
2
+
.
.
.
+
x
M
=
∑
k
=
0
M
x
k
=
1
−
x
M
+
1
1
−
x
,
∣
x
∣
<
1
size 12{1+x+x rSup { size 8{2} } + "." "." "." +x rSup { size 8{M} } = Sum cSub { size 8{k=0} } cSup { size 8{M} } {x rSup { size 8{k} } = { {1 - x rSup { size 8{M+1} } } over {1 - x} } } , matrix {
{} # {} # {}} \lline x \lline<1} {}
here
x
=
a
/
b
size 12{x= {a} slash {b} } {} , we get
h
(
n
)
=
b
n
1
−
(
a
b
)
n
+
1
1
−
a
b
=
b
n
+
1
−
a
n
+
1
b
−
a
size 12{h \( n \) =b rSup { size 8{n} } { {1 - \( { { size 8{a} } over { size 8{b} } } \) rSup { size 8{n+1} } } over {1 - { { size 8{a} } over { size 8{b} } } } } = { {b rSup { size 8{n+1} } - a rSup { size 8{n+1} } } over {b - a} } } {}
Distributivity
It can be shown
x
(
n
)
∗
[
h
1
(
n
)
+
h
2
(
n
)
]
=
x
(
n
)
∗
h
1
(
n
)
+
x
(
n
)
∗
h
2
(
n
)
size 12{x \( n \) * \[ h rSub { size 8{1} } \( n \) +h rSub { size 8{2} } \( n \) \] =x \( n \) * h rSub { size 8{1} } \( n \) +x \( n \) * h rSub { size 8{2} } \( n \) } {}
The system meaning is illustrated in
[link] where two systems connected in parallel can be replaced by one whose impulse response is the sum of the two ones.
Impulse response of two systems in parallel
Impulse response for causal system and signal
Since impulse response is a characterization (among other characterizations) of systems. As such, the causality of a system would be reflected on its impulse response. From the convolution
Figure the output at instant
n
0
size 12{n rSub { size 8{0} } } {} is:
y
(
n
0
)
=
∑
k
=
0
∞
h
(
k
)
x
(
n
0
−
k
)
+
∑
k
=
−
∞
−
1
h
(
k
)
x
(
n
0
−
k
)
size 12{y \( n rSub { size 8{0} } \) = Sum cSub { size 8{k=0} } cSup { size 8{ infinity } } {h \( k \) x \( n rSub { size 8{0} } - k \) } + Sum cSub { size 8{k= - infinity } } cSup { size 8{ - 1} } {h \( k \) x \( n rSub { size 8{0} } - k \) } } {}
In order the output signal
y
(
n
0
)
size 12{y \( n rSub { size 8{0} } \) } {} does not depend on future
(
n
>
n
0
)
size 12{ \( n>n rSub { size 8{0} } \) } {} values of input signal
x
(
n
)
size 12{x \( n \) } {} , the second term of above equation should be zero, i.e.
h
(
k
)
=
0
size 12{h \( k \) =0} {} for
k
<
0
size 12{k<0} {} . As k is a dummy variable, we conclude
h
(
n
)
=
0
at
n
<
0
size 12{h \( n \) =0 matrix {
{} # {}} ital "at" matrix {
{} # {}} n<0} {}
Thus, the causality of a system implies that its impulse response is zero and vice versa. The output at time
n
0
size 12{n rSub { size 8{0} } } {} is now the first term of the equation
y
(
n
0
)
=
∑
k
=
0
∞
h
(
k
)
x
(
n
0
−
k
)
size 12{y \( n rSub { size 8{0} } \) = Sum cSub { size 8{k=0} } cSup { size 8{ infinity } } {h \( k \) x \( n rSub { size 8{0} } - k \) } } {}
For any time n,
y
(
n
)
=
∑
k
=
0
∞
h
(
k
)
x
(
n
−
k
)
(
only
the
signal
is
causal
)
size 12{y \( n \) = Sum cSub { size 8{k=0} } cSup { size 8{ infinity } } {h \( k \) x \( n - k \) } matrix {
{} # {} # {}} \( matrix {
ital "only" {} # ital "the" {} # ital "signal" {} # ital "is" {} # ital "causal"{}} \) } {}
Had the convolution
x
(
n
)
∗
h
(
n
)
size 12{x \( n \) *h \( n \) } {} been used, the result would be
y
(
n
)
=
∑
k
=
−
∞
n
x
(
k
)
h
(
n
−
k
)
(
only
the
signal
is
causal
)
size 12{y \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{n} } {x \( k \) h \( n - k \) } matrix {
{} # {} # {}} \( matrix {
ital "only" {} # ital "the" {} # ital "signal" {} # ital "is" {} # ital "causal"{}} \) } {}
In above, only the causality of the system is considered. Now, the imput signal is also causal, the result is
y
(
n
)
=
∑
k
=
0
n
h
(
k
)
x
(
n
−
k
)
(
both
system
and
signal
are
causal
)
size 12{y \( n \) = Sum cSub { size 8{k=0} } cSup { size 8{n} } {h \( k \) x \( n - k \) } matrix {
{} # {} # {}} \( matrix {
ital "both" {} # ital "system" {} # ital "and" {} # ital "signal" {} # ital "are" {} # ital "causal"{}} \) } {}
And equivalently
y
(
n
)
=
∑
k
=
0
n
x
(
k
)
h
(
n
−
k
)
(
both
system
and
signal
are
causal
)
size 12{y \( n \) = Sum cSub { size 8{k=0} } cSup { size 8{n} } {x \( k \) h \( n - k \) } matrix {
{} # {}} \( matrix {
ital "both" {} # ital "system" {} # ital "and" {} # ital "signal" {} # ital "are" {} # ital "causal"{}} \) } {}
Notice that the summation limits for both cases are the same and the upper limit increases with n, also that the output signal
y
(
n
)
size 12{y \( n \) } {} at time n depends only the convolution summation up to n and independent of future values after n. So we can write the upper limit as
∞
size 12{ infinity } {} without effecting the result.
Input signal and impulse response are respectively
x
(
n
)
=
u
(
n
)
h
(
n
)
=
a
n
u
(
n
)
∣
a
∣
<
1
alignl { stack {
size 12{x \( n \) =u \( n \) } {} #size 12{h \( n \) =a rSup { size 8{n} } u \( n \) matrix {
{} # {} # {} # {}} \lline a \lline<1} {}
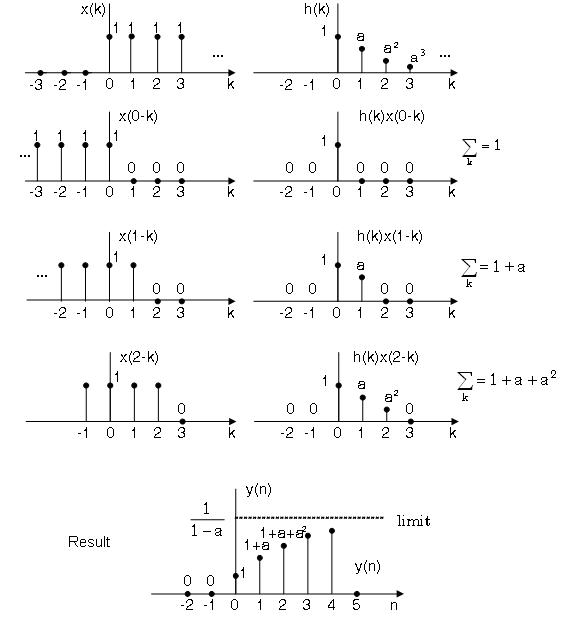
} } {} Find the output signal by analysis computation.
Solution
Notice that both
x
(
n
)
size 12{x \( n \) } {} and
h
(
n
)
size 12{h \( n \) } {} are causal and of infinite duration. The given condition
∣
a
∣
<
1
size 12{ lline a rline<1} {} ensures the convergence of
h
(
n
)
size 12{h \( n \) } {} . We choose to evaluate
h
(
n
)
∗
x
(
n
)
size 12{h \( n \) *x \( n \) } {} , using
[link]
y
(
n
)
=
h
(
n
)
∗
x
(
n
)
=
∑
k
=
−
∞
∞
h
(
k
)
x
(
n
−
k
)
=
∑
k
=
0
n
a
k
u
(
k
)
u
(
n
−
k
)
=
∑
k
=
0
n
a
k
alignl { stack {
size 12{y \( n \) =h \( n \) * x \( n \) = Sum cSub { size 8{k= - infinity } } cSup { size 8{ infinity } } {h \( k \) x \( n - k \) = Sum cSub { size 8{k=0} } cSup { size 8{n} } {a rSup { size 8{k} } u \( k \) u \( n - k \) } } } {} #matrix {
matrix {{} # {} # {} # {}
} {} # {} # {} # {}} matrix {
{} # {} # {} # {}} matrix {
{} # {}} = Sum cSub { size 8{k=0} } cSup { size 8{n} } {a rSup { size 8{k} } } {}
} } {}
So, the result is.
y
(
0
)
=
1
y
(
1
)
=
1
+
a
y
(
2
)
=
1
+
a
+
a
2
.
.
.
y
(
n
)
=
1
+
a
+
a
2
+
.
.
.
+
a
n
alignl { stack {
size 12{y \( 0 \) =1} {} #size 12{y \( 1 \) =1+a} {} #
size 12{y \( 2 \) =1+a+a rSup { size 8{2} } } {} #"." "." "." {} #
y \( n \) =1+a+a rSup { size 8{2} } + "." "." "." +a rSup { size 8{n} } {}} } {}
The output signal
y
(
n
)
size 12{y \( n \) } {} does not go to
∞
size 12{ infinity } {} but grows asymptotically to the finite value of
1
1
−
a
size 12{ { {1} over {1 - a} } } {} (see
Example ).
System identification
In DSP sometimes we need to determine a system, assumed LTI (or LSI), when we know the input signal and output signal, e.g. by setting up an experiment. This problem is called
system identification . Specifically, we must determine the impulse response of the system, and then the signal difference equation if necessary.
Adaptive filters using FIR filters are often used to identify unknown DSP systems. In control theory, also, sytem identification is a familiar problem.
For causal systems the output is given by the reduced convolution (
[link] ) which is repeated here
y
(
n
)
=
∑
k
=
0
n
h
(
k
)
x
(
n
−
k
)
,
n
≥
0
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacaGGOaGaamOBaiaacMcacqGH9aqpdaaeWbqaaiaadIgacaGGOaGaam4AaiaacMcacaWG4bGaaiikaiaad6gacqGHsislcaWGRbGaaiykaiaaysW7caGGSaGaaGzbVlaad6gacqGHLjYScaaIWaaaleaacaWGRbGaeyypa0JaaGimaaqaaiaad6gaa0GaeyyeIuoaaaa@4FA2@
At
n
=
0
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaad6gacqGH9aqpcaaIWaaaaa@3886@
y
(
0
)
=
h
(
0
)
x
(
0
)
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacaGGOaGaaGimaiaacMcacqGH9aqpcaWGObGaaiikaiaaicdacaGGPaGaamiEaiaacIcacaaIWaGaaiykaaaa@3FFA@
giving
h
(
0
)
=
y
(
0
)
x
(
0
)
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaaGimaiaacMcacqGH9aqpdaWcaaqaaiaadMhacaGGOaGaaGimaiaacMcaaeaacaWG4bGaaiikaiaaicdacaGGPaaaaaaa@400A@
provided
x
(
0
)
≠
0
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhacaGGOaGaaGimaiaacMcacqGHGjsUcaaIWaaaaa@3B64@ . At
n
≥
1
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaad6gacqGHLjYScaaIXaaaaa@3947@ , We can write
y
(
n
)
=
h
(
n
)
x
(
0
)
+
∑
k
=
0
n
−
1
h
(
k
)
x
(
n
−
k
)
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacaGGOaGaamOBaiaacMcacqGH9aqpcaWGObGaaiikaiaad6gacaGGPaGaamiEaiaacIcacaaIWaGaaiykaiabgUcaRmaaqahabaGaamiAaiaacIcacaWGRbGaaiykaiaadIhacaGGOaGaamOBaiabgkHiTiaadUgacaGGPaaaleaacaWGRbGaeyypa0JaaGimaaqaaiaad6gacqGHsislcaaIXaaaniabggHiLdaaaa@5137@
giving
h
(
n
)
=
y
(
n
)
−
∑
k
=
0
n
−
1
h
(
k
)
x
(
n
−
k
)
x
(
0
)
,
n
≥
1
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaamOBaiaacMcacqGH9aqpdaWcaaqaaiaadMhacaGGOaGaamOBaiaacMcacqGHsisldaaeWbqaaiaadIgacaGGOaGaam4AaiaacMcacaWG4bGaaiikaiaad6gacqGHsislcaWGRbGaaiykaaWcbaGaam4Aaiabg2da9iaaicdaaeaacaWGUbGaeyOeI0IaaGymaaqdcqGHris5aaGcbaGaamiEaiaacIcacaaIWaGaaiykaaaacaaMe8UaaiilaiaaywW7caWGUbGaeyyzImRaaGymaaaa@589B@
In order to identify an unknown DSP system (hardware or software) we applied a signal x(n) and obtained the output y(n) as follows.
x
(
n
)
=
[
1
,
2
,
−
1
,
−
2
,
1
,
2
]
y
(
n
)
=
[
0
,
1
,
4
,
3
,
−
4
,
−
3
,
4
,
4
]
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOabaeqabaGaamiEaiaacIcacaWGUbGaaiykaiabg2da9iaacUfaieqacaWFXaGaaiilaiaaysW7caaIYaGaaiilaiaaysW7cqGHsislcaaIXaGaaiilaiaaysW7cqGHsislcaaIYaGaaiilaiaaysW7caaIXaGaaiilaiaaysW7caaIYaGaaiyxaaqaaiaadMhacaGGOaGaamOBaiaacMcacqGH9aqpcaGGBbGaa8hmaiaacYcacaaMe8UaaGymaiaacYcacaaMe8UaaGinaiaacYcacaaMe8UaaG4maiaacYcacaaMe8UaeyOeI0IaaGinaiaacYcacaaMe8UaeyOeI0IaaG4maiaacYcacaaMe8UaaGinaiaacYcacaaMe8UaaGinaiaac2faaaaa@6ACD@
Determine the impulse response.
Solution
Note that both input and output signals are causal. We proceed the evaluation of the impulse response as follows.
h
(
0
)
=
y
(
0
)
x
(
0
)
=
0
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaaGimaiaacMcacqGH9aqpdaWcaaqaaiaadMhacaGGOaGaaGimaiaacMcaaeaacaWG4bGaaiikaiaaicdacaGGPaaaaiabg2da9iaaicdaaaa@41CA@
h
(
1
)
=
y
(
1
)
−
h
(
0
)
x
(
1
)
x
(
0
)
=
1
−
0
(
2
)
1
=
1
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaaGymaiaacMcacqGH9aqpdaWcaaqaaiaadMhacaGGOaGaaGymaiaacMcacqGHsislcaWGObGaaiikaiaaicdacaGGPaGaamiEaiaacIcacaaIXaGaaiykaaqaaiaadIhacaGGOaGaaGimaiaacMcaaaGaeyypa0ZaaSaaaeaacaaIXaGaeyOeI0IaaGimaiaacIcacaaIYaGaaiykaaqaaiaaigdaaaGaeyypa0JaaGymaaaa@4F13@
h
(
2
)
=
y
(
2
)
−
h
(
0
)
x
(
2
)
−
h
(
1
)
x
(
1
)
x
(
0
)
=
4
−
0
(
−
1
)
−
1
(
2
)
1
=
2
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaaGOmaiaacMcacqGH9aqpdaWcaaqaaiaadMhacaGGOaGaaGOmaiaacMcacqGHsislcaWGObGaaiikaiaaicdacaGGPaGaamiEaiaacIcacaaIYaGaaiykaiabgkHiTiaadIgacaGGOaGaaGymaiaacMcacaWG4bGaaiikaiaaigdacaGGPaaabaGaamiEaiaacIcacaaIWaGaaiykaaaacqGH9aqpdaWcaaqaaiaaisdacqGHsislcaaIWaGaaiikaiabgkHiTiaaigdacaGGPaGaeyOeI0IaaGymaiaacIcacaaIYaGaaiykaaqaaiaaigdaaaGaeyypa0JaaGOmaaaa@5AC2@
h
(
3
)
=
y
(
3
)
−
h
(
0
)
x
(
3
)
−
h
(
1
)
x
(
2
)
−
h
(
2
)
x
(
1
)
x
(
0
)
=
3
−
0
(
−
2
)
−
1
(
−
1
)
−
2
(
2
)
1
=
0
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaaG4maiaacMcacqGH9aqpdaWcaaqaaiaadMhacaGGOaGaaG4maiaacMcacqGHsislcaWGObGaaiikaiaaicdacaGGPaGaamiEaiaacIcacaaIZaGaaiykaiabgkHiTiaadIgacaGGOaGaaGymaiaacMcacaWG4bGaaiikaiaaikdacaGGPaGaeyOeI0IaamiAaiaacIcacaaIYaGaaiykaiaadIhacaGGOaGaaGymaiaacMcaaeaacaWG4bGaaiikaiaaicdacaGGPaaaaiabg2da9maalaaabaGaaG4maiabgkHiTiaaicdacaGGOaGaeyOeI0IaaGOmaiaacMcacqGHsislcaaIXaGaaiikaiabgkHiTiaaigdacaGGPaGaeyOeI0IaaGOmaiaacIcacaaIYaGaaiykaaqaaiaaigdaaaGaeyypa0JaaGimaaaa@666E@
Continuing we will see that for . Thus the system impulse response is
h
(
n
)
=
[
0
,
1
,
2
]
MathType@MTEF@5@5@+=feaagaart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiFCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgacaGGOaGaamOBaiaacMcacqGH9aqpcaGGBbacbeGaa8hmaiaacYcacaaMe8UaaGymaiaacYcacaaMe8UaaGOmaiaac2faaaa@427E@
The system is causal as expected.
Another method is to transform the problem to the z-domain (chapter 4).