4.5 Venn diagrams (optional)

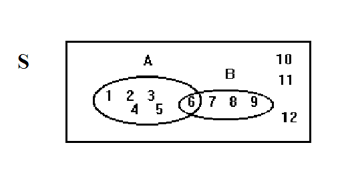
Suppose an experiment has the outcomes 1, 2, 3, ... , 12 where each outcome has an equal chance of occurring. Let event $A=\text{{1, 2, 3, 4, 5, 6}}$ and event $B=\text{{6, 7, 8, 9}}$ . Then $\mathrm{A AND B}=\text{{6}}$ and $\mathrm{A OR B}=\text{{1, 2, 3, 4, 5, 6, 7, 8, 9}}$ . The Venn diagram is as follows:

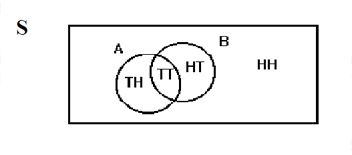
Flip 2 fair coins. Let $A$ = tails on the first coin. Let $B$ = tails on the second coin. Then $A=\{\mathrm{TT},\mathrm{TH}\}$ and $B=\{\mathrm{TT},\mathrm{HT}\}$ . Therefore, $\text{A AND B}=\left\{\mathrm{TT}\right\}$ . $\text{A OR B}=\{\mathrm{TH},\mathrm{TT},\mathrm{HT}\}$ .

The sample space when you flip two fair coins is $S=\{\mathrm{HH},\mathrm{HT},\mathrm{TH},\mathrm{TT}\}$ . The outcome $\mathrm{HH}$ is in neither $A$ nor $B$ . The Venn diagram is as follows:

Forty percent of the students at a local college belong to a club and 50% work part time. Five percent of the students work part time and belong to a club. Draw a Venn diagram showing the relationships. Let $C$ = student belongs to a club and $\mathrm{PT}$ = student works part time.

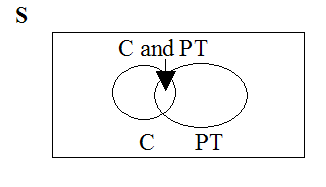
If a student is selected at random find

• The probability that the student belongs to a club. $\text{P(C)}=0.40$ .
• The probability that the student works part time. $\text{P(PT)}=0.50$ .
• The probability that the student belongs to a club AND works part time. $\text{P(C AND PT)}=0.05$ .
• The probability that the student belongs to a club given that the student works part time.
  $\text{P(C|PT)} = \frac{\text{P(C AND PT)}}{\text{P(PT)}} = \frac{0.05}{0.50} = 0.1$
• The probability that the student belongs to a club OR works part time.
  $\text{P(C OR PT)}=\text{P(C)}+\text{P(PT)}-\text{P(C AND PT)}=0.40+0.50-0.05=0.85$