| << Chapter < Page | Chapter >> Page > |
Solving for gives
Because a long uniform wire is used for , the ratio of resistances is the same as the ratio of the lengths of wire that zero the galvanometer for each emf. The three quantities on the right-hand side of the equation are now known or measured, and can be calculated. The uncertainty in this calculation can be considerably smaller than when using a voltmeter directly, but it is not zero. There is always some uncertainty in the ratio of resistances and in the standard . Furthermore, it is not possible to tell when the galvanometer reads exactly zero, which introduces error into both and , and may also affect the current .
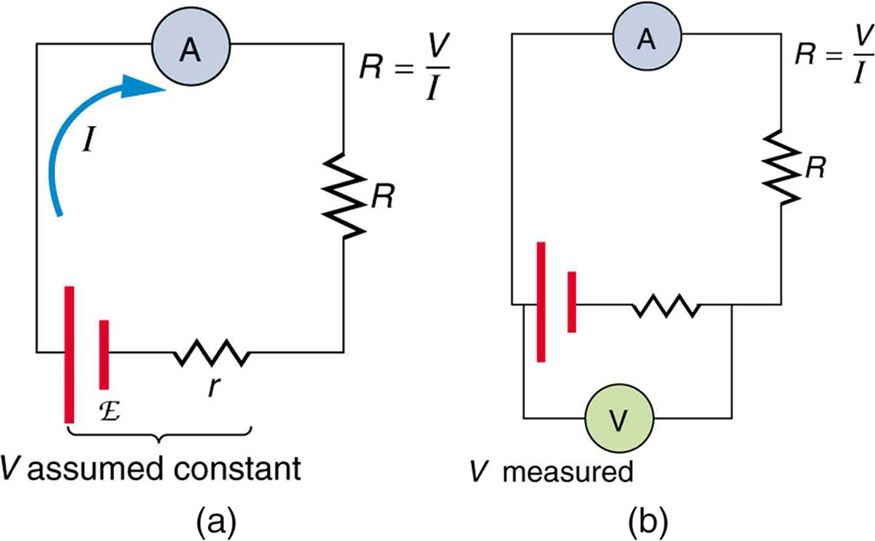
There is a variety of so-called ohmmeters that purport to measure resistance. What the most common ohmmeters actually do is to apply a voltage to a resistance, measure the current, and calculate the resistance using Ohm’s law. Their readout is this calculated resistance. Two configurations for ohmmeters using standard voltmeters and ammeters are shown in [link] . Such configurations are limited in accuracy, because the meters alter both the voltage applied to the resistor and the current that flows through it.
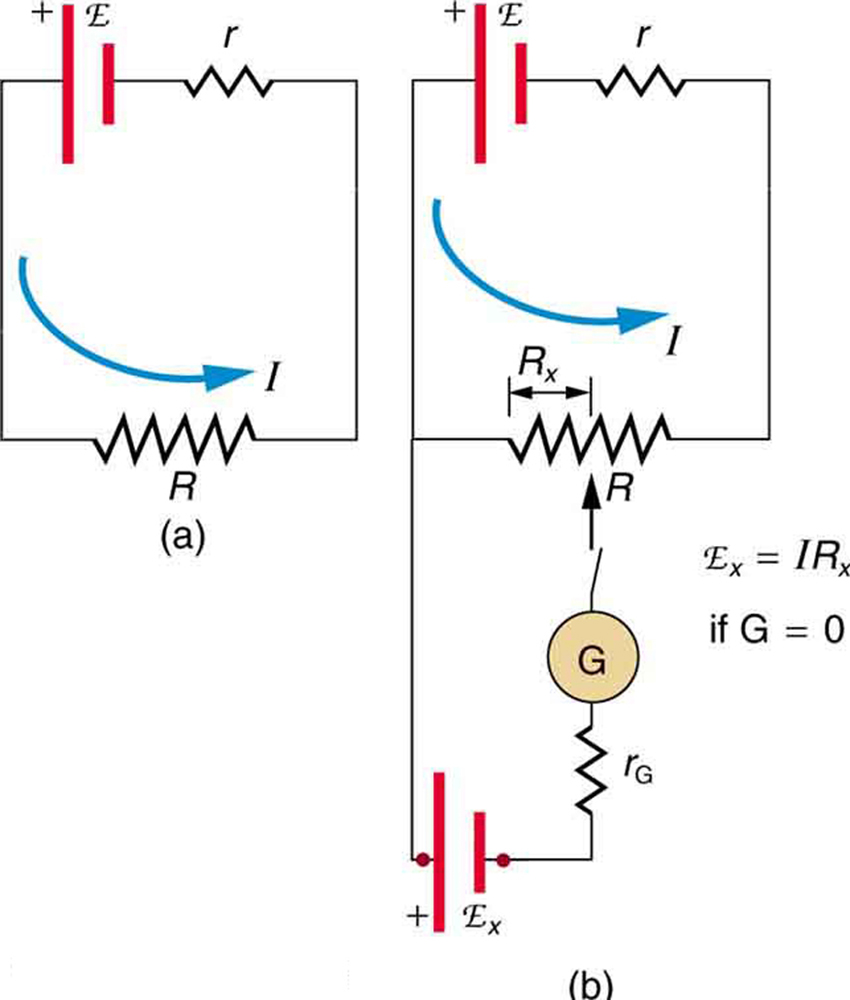
The Wheatstone bridge is a null measurement device for calculating resistance by balancing potential drops in a circuit. (See [link] .) The device is called a bridge because the galvanometer forms a bridge between two branches. A variety of bridge devices are used to make null measurements in circuits.
Resistors and are precisely known, while the arrow through indicates that it is a variable resistance. The value of can be precisely read. With the unknown resistance in the circuit, is adjusted until the galvanometer reads zero. The potential difference between points b and d is then zero, meaning that b and d are at the same potential. With no current running through the galvanometer, it has no effect on the rest of the circuit. So the branches abc and adc are in parallel, and each branch has the full voltage of the source. That is, the drops along abc and adc are the same. Since b and d are at the same potential, the drop along ad must equal the drop along ab. Thus,

Notification Switch
Would you like to follow the 'College physics ii' conversation and receive update notifications?