| << Chapter < Page | Chapter >> Page > |
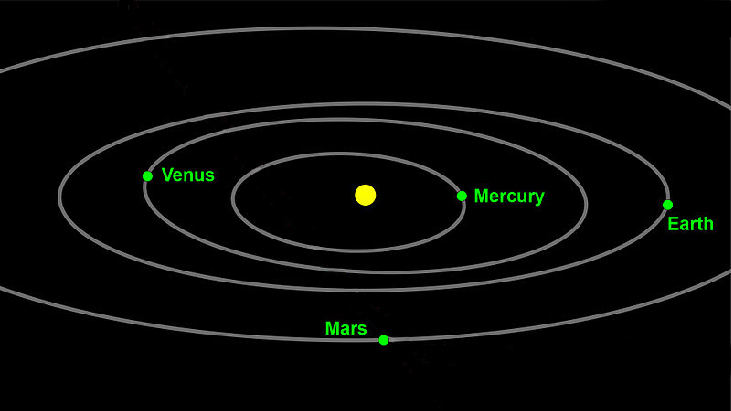
The planets move through space in elliptical, periodic orbits about the sun, as shown in [link] . They are in constant motion, so fixing an exact position of any planet is valid only for a moment. In other words, we can fix only a planet’s instantaneous position. This is one application of polar coordinates , represented as We interpret as the distance from the sun and as the planet’s angular bearing, or its direction from a fixed point on the sun. In this section, we will focus on the polar system and the graphs that are generated directly from polar coordinates.
Just as a rectangular equation such as describes the relationship between and on a Cartesian grid, a polar equation describes a relationship between and on a polar grid. Recall that the coordinate pair indicates that we move counterclockwise from the polar axis (positive x -axis) by an angle of and extend a ray from the pole (origin) units in the direction of All points that satisfy the polar equation are on the graph.
Symmetry is a property that helps us recognize and plot the graph of any equation. If an equation has a graph that is symmetric with respect to an axis, it means that if we folded the graph in half over that axis, the portion of the graph on one side would coincide with the portion on the other side. By performing three tests, we will see how to apply the properties of symmetry to polar equations. Further, we will use symmetry (in addition to plotting key points, zeros, and maximums of to determine the graph of a polar equation.
In the first test, we consider symmetry with respect to the line ( y -axis). We replace with to determine if the new equation is equivalent to the original equation. For example, suppose we are given the equation
This equation exhibits symmetry with respect to the line
In the second test, we consider symmetry with respect to the polar axis ( -axis). We replace with or to determine equivalency between the tested equation and the original. For example, suppose we are given the equation
The graph of this equation exhibits symmetry with respect to the polar axis.
In the third test, we consider symmetry with respect to the pole (origin). We replace with to determine if the tested equation is equivalent to the original equation. For example, suppose we are given the equation
The equation has failed the symmetry test , but that does not mean that it is not symmetric with respect to the pole. Passing one or more of the symmetry tests verifies that symmetry will be exhibited in a graph. However, failing the symmetry tests does not necessarily indicate that a graph will not be symmetric about the line the polar axis, or the pole. In these instances, we can confirm that symmetry exists by plotting reflecting points across the apparent axis of symmetry or the pole. Testing for symmetry is a technique that simplifies the graphing of polar equations, but its application is not perfect.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?