| << Chapter < Page | Chapter >> Page > |
.
AKTIWITEIT 2
Om waarskynlikhede in sekere kontekste te bereken
[LU 1.2, 1.4, 1.7, 5.4, 5.6]
Enkelvoudige eksperimente
1 Daar is 12 balle in ’n sak: 3 blou, 5 groen, 3 wit en een rooi bal.
1.1 Bereken die waarskynlik dat óf ’n groen óf ’n blou bal uitgehaal sal word.
1.2 Wat is die waarskynlikheid dat ’n geel bal gekies word?
2 ’n Gewone dobbelsteen word gegooi. Bereken die waarskynlikheid van:
2.1 ’n twee 2.2 ’n onewe getal 2.3 ’n getal wat groter as twee is.
Saamgestelde eksperimente.
3 Beskou die opskiet van ’n muntstuk – die resultaat kan óf kruis óf munt wees.
Ons moet eers bepaal wat die totale aantal uitkomste moontlik kan wees. Ons kry (a) kruis gevolg deur kruis, of (b) kruis gevolg deur munt; of dalk (c) munt gevolg deur kruis, of (d) munt gevolg deur munt.
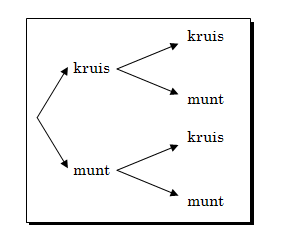
Die diagram wys dit as ’n boom. Daar is dus vier moontlike uitkomste. Twee munte ná mekaar gebeur slegs eenkeer uit die vier. Dus is die waarskynlikheid daarvan of 0,25.
Werk uit:
3.1 Wat is die waarskynlikheid dat jy twee verskillende kante van die muntstuk na mekaar sal kry?
4 Nog voorbeelde uit die sak met balle:
As jy dit doen, wat is die waarskynlikheid dat jy al twee keer blou balle sal uithaal?
4.1 Teken die boomdiagram vir hierdie situasie.
Ons kan nou sien dat die totale aantal uitkomste 16 is! Van hulle is slegs één BB, dus is ons waarskynlikheid 116 = 0,063. Bereken die waarskynlikheid van
4.2 twee balle van dieselfde kleur.
4.3 twee balle met verskillende kleure.
4.4 ten minste een wit bal.
4.5 ’n blou bal met die tweede trekking.
4.6 ’n geel bal.
4.7 geen rooi balle.
AKTIWITEIT 3
Om te begryp dat kennis van risiko’s belangrik is vir lewensbesluite

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?