| << Chapter < Page | Chapter >> Page > |
1.2 Hoe sou jy sê: Is Gabriel of James die slimste?
1.3 As die vriende beide dieselfde salaris verdien en dieselfde verhogings kry, wie het die meeste geld elke maand oor om op ander noodsaaklikhede of plesiertjies uit te gee?
1.4 Gebruik die waardes in die tabel en bereken hoeveel elke jong man in totaal uitgegee het aan die aankoop van motors gedurende die hele tydperk van 2000 tot 2013.
1.5 As jy begin werk en jou pa bied jou sy ou motor (wat nog steeds lekker loop) aan as ’n geskenk, sou jy dit aanvaar en begin spaar vir ’n nuwe motor soos Gabriel, of sou jy dit bedank en dadelik ’n nuwe motor op huurkoop koop soos James? Verduidelik jou antwoord.
1.6 Gaan gesels met ’n verkoopsman wat nuwe motors verkoop en vra hom om presies te verduidelik waaraan jy moet voldoen voordat jy ’n huurkoopooreenkoms kan aangaan. Vra ook oor versekering, wie die motor besit, en wat gebeur as jy nie kan voortgaan met die paaiemente nie.
2 Reguitlyngrafieke met positiewe gradiënte toon ’n direkte verband tussen twee veranderlikes. Sommige grafieke toon ’n omgekeerde verband tussen twee veranderlikes. Ons bekyk twee situasies waar hierdie soort verband voorkom.
2.1 Eerstens ’n geval wat ons weer sal teëkom in die deel oor waarskynlikheidsleer:
Hier is die puntediagram vir die drie-steentjie spel, en een vir vier steentjies.
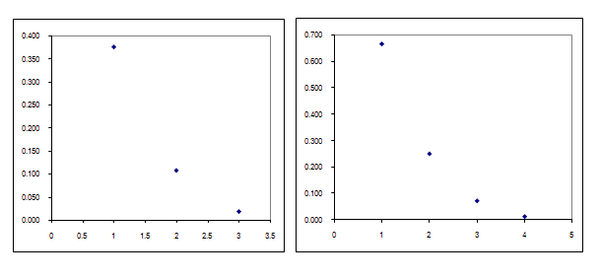
2.2 Nog ’n praktiese voorbeeld van hierdie verband:
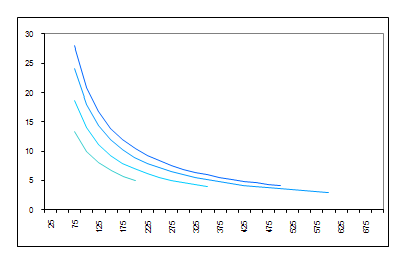
Hier is ’n grafiek wat die kostes van die verskillende sale vergelyk. Afhangende daarvan hoeveel mense die sokkie bywoon (op die horisontale as), toon die vertikale as die koste per persoon. Hulle wil ten minste R4 000 vir die liefdadigheid insamel, maar sou verkies dat dit R5 000 moet wees.
a) Kan jy uitwerk watter lyn na watter saal verwys? As jy die aantal mense wat in die saal kan pas in ag neem, is dit maklik!
b) Gebruik nou al hierdie inligting en die grafieke en besluit watter saal die beste keuse sou wees. Almal hoef nie noodwendig dieselfde antwoord te kry nie, maar jy moet jou antwoord met goeie argumente staaf.
3 Hier is die tabel met toetspunte weer:

Notification Switch
Would you like to follow the 'Wiskunde graad 9' conversation and receive update notifications?