3.5 To solve problems in context

Mathematics

Measurement and time

Length

Educator section

Memorandum

1. Susan = 3,48

Lala = 3,4

Lauren = 3,2

Anna = 3,12

2. Susan: (2,32 + 3,48 + 3,02 + 2,9) ÷ 4 = 2,93 (2,9 m)

Lala: (3,2 + 3,04 + 2,86 + 3,4) ÷ 4 = 3,125 (3,1 m)

Lauren: (2,88 + 2,96 + 3,06 + 3,2) ÷ 4 = 3,025 (3 m)

Anna: (3,02 + 2,94 + 2,84 + 3,12) ÷ 4 = 2,98 (3 m)

3. (12,95 km + 14,73 km + 8,94 km + 13,8 km + 6,86 km) ÷ 5

= 11,456 km (11,5 km)

4. 11,5 km

Leaner section

Content

Activity: to solve problems in context [lo 1.6.2]

It is important to be able to calculate averages, because it is something that is commonly used in everyday life. You have heard of average rainfall per month, the average temperature of the place where you live during a particular season, your class average, etc.

1. Take a good look at the following and then write down what the distance of the best jump of each athlete is:

At an athletics meeting four athletes participated in the u.13 long jump for girls.

Each completed four jumps.

• By looking at each girl’s best jump, we can determine who won.
• However, this does not tell us who fared the best in general (over all the jumps).
• To determine this we have to look at the average of each girl’s jumps.
• The following is the formula for calculating the average:

Average distance =

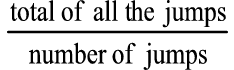
In Susan’s case it will be calculated as follows:

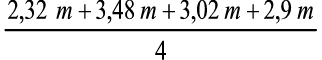
= 2,93 m (rounded off to the first decimal: 2,9 m)

2. Now use this formula to determine, according to the averages for the four athletes, who generally fared the best in the long jump for u.13 girls (rounded off to the first decimal).

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

3. Calculate the average distance that Johan runs per day if he ran the following distances from Monday to Friday:

Mon. 12,95 km; Tue. 14,73 km; Wed. 8,94 km; Thu. 13,8 km; Fri. 6,86 km.

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

_____________________________________________________________________

4. Round off your answer to the first decimal place.

_____________________________________________________________________

Time for self-assessment

We examined particular aspects of measuring in Learning Unit 1. Before starting to work through Learning Unit 2, we have to find out whether there are any hitches, i.e. whether there is anything that you do not understand properly. Show us how you feel about the completed work by neatly colouring the blocks that represent your feelings about the work:

CRITERIA

Assessment

Learning Outcome 1: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.

Assessment Standard 1.6: We know this when the learner solves problems in context including contexts that may be used to build awareness of other Learning Areas, as well as human rights, social, economic and environmental issues such as:

1.6.2: measurements in Natural Sciences and Technology contexts.