| << Chapter < Page | Chapter >> Page > |
1.18. THE CORRECT INTERPRETATION OF KINETIC THEORY OF GASES BASED ON QUANTUM MECHANICS.
A thermally isolated system is known as an adiabatic system. In an adiabatic expansion we have the following law:
PV γ = Constant …………………………………………………………. 1.172
PV=kT …………………………………………………………… 1.173
PV=(γ-1)U where U(internal energy)=(3/2)kT ………………………………………………………………………………………………………… 1.174
According to equipartition law of energy with every degree of freedom the average thermal energy associated is (1/2)kT.
A monoatomic molecule has only three translational degrees of freedom. Hence the average thermal energy associated:
U = (3/2)kT
Or kT = (2U)/3
Therefore in a monoatomic molecule gas from Eq.(1.173) and Eq.(1.174):
(γ-1) = (2/3)
or γ = 1+ (2/3) = (5/3) = 1.667
In a diatomic molecular gas, there are three degrees of freedom for translation, two degrees of freedom for spin around its longtitudinal axis and transverse axis and two degrees of freedom for vibration. Therefore total internal energy is:
U= (3/2 + 2/2 + 2/2)kT = (7/2)kT
Or kT = (2/7)U
Therefore in a diatomic gas again from Eq.(1.173) and Eq.(1.174):
(γ-1) = (2/7)
or γ = (9/7) = 1.286
Experimentally observed values of the adiabatic constant is tabulated in Table(1.34). The observed values of adiabatic constant cannot be explained on the basis of Classical Physics. Here again Quantum Physics comes to our rescue.
Table.1.34 Adiabatic Constants for different gas systems
| Gas | T(°Celsius) | γ |
| He | -180 | 1.660 |
| Kr | 19 | 1.68 |
| H 2 | 100 | 1.404 |
| Br 2 | 300 | 1.32 |
| I 2 | 185 | 1.3 |
| C 2 H 6 | 15 | 1.22 |
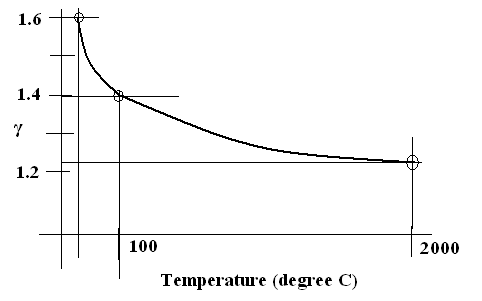
Figure 1.92 Variation of Adiabatic Constant with temperature for a given gas system.
According to Classical Physics many molecules can stay in the same energy state in the same volume. But according to Quantum Mechanics this is not permissible.
In a mono-atomic gas there are only three degrees of freedom of translation are available and these degrees of freedom is constant . Hence Adiabatic Constant is uniform with variation with temperature. This is found experimentally correct. But in diatomic molecules or multiatomic molecules this is not true.
Let us take diatomic molecule Hydrogen. At high temperature it has seven degrees of freedom. Two vibrational degrees of freedom, two degrees of freedom in rotational motion one is spin rotation and the other is orbital rotation and three degrees of freedom of translation . But as the temperature is reduced it loses the vibrational degrees of freedom and subsequently it loses rotational degrees of freedom. At low temperature only translational degrees of freedom remain. Therefore Adiabatic Constant is 1.6 at 25 degree Celsius. This falls to 1.4 at 100 degree Celsius. This further falls to 1.286 at 2000 degree Celsius.
The experimentally observed Adiabatic Constant variation with temperature as shown in Figure 1.92 is the most convincing vindication of the correctness of Quantum Physics at molecular scale.
Stefan- Boltzmann Law gives the total energy emitted by a Black-Body Radiator to be:
E T = σ T 4 …………………………………………………………………………. 1.175
Classical Physics has no theoretical explanation for this Fourth Power Law. Quantum Mechanics gives the theoretical value of σ which is:
σ = (2π 5 k 4 )/(1.5c 2 h 3 ) ……………………………………………………………. 1.176
We saw Wien’s Displacement Law in Black Body Radiation:
That is λ m = Ω/T ………………………………………………………………… 1.177
Classical Physics cannot arrive at the theoretical value of Ω. But Quantum Physics gives an elegant theoretical explanation of Black Body Radiation and arrives at the theoretical value of the constant : Ω = ch/(4.9651k)
where c= 3×10 8 m/sec= velocity of light in vacuum,
h= 6.626×10 -34 J.sec= Planck’s Constant,
k = 1.38×10 -23 J/Kelvin;
Substituting the Universal Constants in the above Equation:
The constant in Eq.(1.177) Ω = 3×10 -3 m.Kelvin;
Rewriting Eq.(1.177) λ m = (3×10 -3 /T) m …………………………………………… 1.178
At 3Kelvin we observe 0.1cm microwave radiation pervading the whole Universe. This is called 3Kelvin Cosmic Microwave Background Radiation.
In Molar Specefic Heat theoretical formulation also, Classical Theory has no consistent model. Only Quantum Mechanics can give a consistent model.
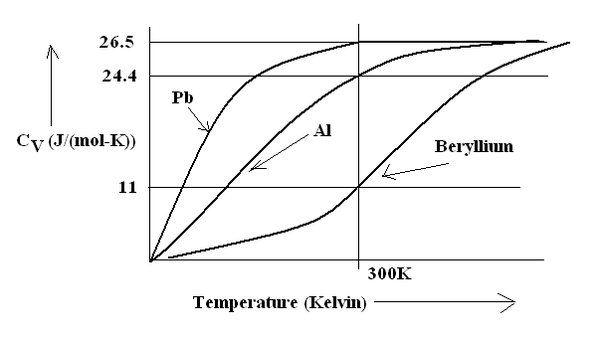
Figure(1.93) Molar Specific Heat variation with temperature in Kelvin.
Table 1.35. Molar Specific Heat at 300 Kelvin for different monoatomic elements.
| Elemental Solids | Molar Specefic Heat ( at 300Kelvin) |
| Pb | 26.5 |
| W | 24.8 |
| Ag | 25.5 |
| Cu | 24.5 |
| Al | 24.4 |
| Beryllium | 11 |
| Boron | 13 |
| Carbon(Carbon) | 6 |
Average Kinetic Energy per degree of freedom = (1/2)kT;
Average Potential Energy per degree of freedom = (1/2)kT;
Since we have monoatomic elements therefore there are only three degrees of freedom of translational motion.
Therefore Molar Heat Q= N A (3kT);
Therefore Molar Heat Capacity= dQ/dT = 3 N A k=3R
where R- Rydberg Constant and N A = Avogadro’s Number;
Substituting the Universal Constants:
Molar Specific Heat of a given material =
Molar Heat Capacity of the given material/Molar Heat Capacity of water=24.93 J/(Mol.K) ;
Therefore all Monoatomic elements should have Molar Specific Heat= 24.93J/(Mol.K).

Notification Switch
Would you like to follow the 'Solid state physics and devices-the harbinger of third wave of civilization' conversation and receive update notifications?