| << Chapter < Page | Chapter >> Page > |
Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall from Right Triangle Trigonometry that, if the sum of two positive angles is those two angles are complements, and the sum of the two acute angles in a right triangle is so they are also complements. In [link] , notice that if one of the acute angles is labeled as then the other acute angle must be labeled
Notice also that opposite over hypotenuse. Thus, when two angles are complimentary, we can say that the sine of equals the cofunction of the complement of Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.
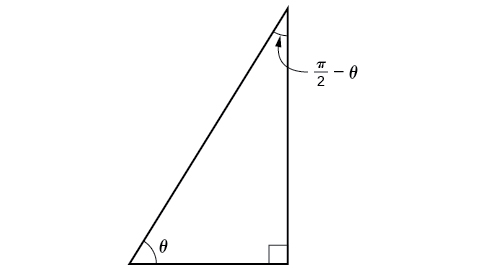
From these relationships, the cofunction identities are formed.
Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using
we can write
Write in terms of its cofunction.
The cofunction of Thus,
Write in terms of its cofunction.
Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems. Reviewing the general rules from Solving Trigonometric Equations with Identities may help simplify the process of verifying an identity.
Given an identity, verify using sum and difference formulas.
Verify the identity
We see that the left side of the equation includes the sines of the sum and the difference of angles.
We can rewrite each using the sum and difference formulas.
We see that the identity is verified.
Verify the following identity.
We can begin by rewriting the numerator on the left side of the equation.
We see that the identity is verified. In many cases, verifying tangent identities can successfully be accomplished by writing the tangent in terms of sine and cosine.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?