5.2 Right triangle trigonometry

We have previously defined the sine and cosine of an angle in terms of the coordinates of a point on the unit circle intersected by the terminal side of the angle:

In this section, we will see another way to define trigonometric functions using properties of right triangles .

Using right triangles to evaluate trigonometric functions

In earlier sections, we used a unit circle to define the trigonometric functions . In this section, we will extend those definitions so that we can apply them to right triangles. The value of the sine or cosine function of $t$ is its value at $t$ radians. First, we need to create our right triangle. [link] shows a point on a unit circle of radius 1. If we drop a vertical line segment from the point $(x,y)$ to the x -axis, we have a right triangle whose vertical side has length $y$ and whose horizontal side has length $x.$ We can use this right triangle to redefine sine, cosine, and the other trigonometric functions as ratios of the sides of a right triangle.

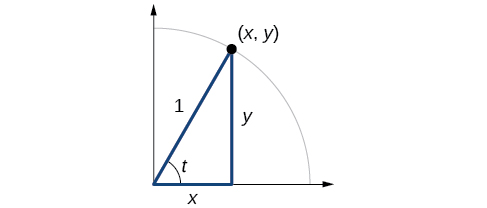
We know

Likewise, we know

These ratios still apply to the sides of a right triangle when no unit circle is involved and when the triangle is not in standard position and is not being graphed using $(x,y)$ coordinates. To be able to use these ratios freely, we will give the sides more general names: Instead of $x,$ we will call the side between the given angle and the right angle the adjacent side    to angle $t.$ (Adjacent means “next to.”) Instead of $y,$ we will call the side most distant from the given angle the opposite side    from angle $t.$ And instead of $1,$ we will call the side of a right triangle opposite the right angle the hypotenuse    . These sides are labeled in [link] .

Understanding right triangle relationships

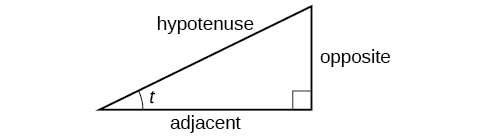
Given a right triangle with an acute angle of $t,$

A common mnemonic for remembering these relationships is SohCahToa, formed from the first letters of “ S ine is o pposite over h ypotenuse, C osine is a djacent over h ypotenuse, T angent is o pposite over a djacent.”

Evaluating a trigonometric function of a right triangle

Given the triangle shown in [link] , find the value of $\cos \alpha .$

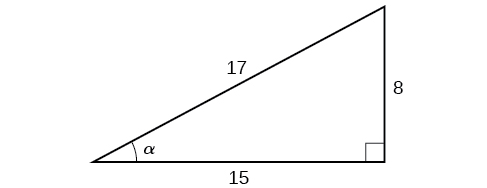
The side adjacent to the angle is 15, and the hypotenuse of the triangle is 17, so:

$$\begin{array}{l}\cos (\alpha )=\frac{\text{adjacent}}{\text{hypotenuse}}\hfill \\ =\frac{15}{17}\hfill \end{array}$$

Try It

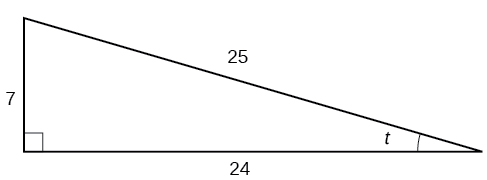
Given the triangle shown in [link] , find the value of $\text{sin}t.$

$\frac{7}{25}$