| << Chapter < Page | Chapter >> Page > |
Во Основни теореми на диференцијалното сметање воведени се поимите за локален екстрем. Така, функцијата има локален минимум (максимум) во точката ако вредноста е помала (поголема) од блиските вредности на функцијата кои и претходат или следуваат после оваа вредност на функцијата.
За разлика од локалниот минимум (максимум) на функција, постои и апсолутен минимум (максимум), а тоа е најмалата (најголемата) вредност на функцијата која ја добива на целиот интервал на кој таа се разгледува.
На Сл. 1 е прикажан графикот на функцијата на затворениот интервал . На овој интервал се испитуваат вредностите на функцијата во локалните екстреми и вредностите на функцијата на краевите од интервалот. Забележуваме дека функцијата има локален максимум во точката со вредност на функцијата , а локалниот минимум е во точката со вредност на функцијата . Вредностите на функцијата на краевите од интервалот се и . Апсолутен минимум е најмалата вредност на функцијата од сите овие вредности, а тоа е локланиот минимум т.е. . Апсолутниот максимум е најголемата од сите вредности на функцијата, а во наведениот пример тоа е . Гледаме дека апсолутен екстрем може да се постигне или во локален екстрем или на еден од краевите на интервалот.
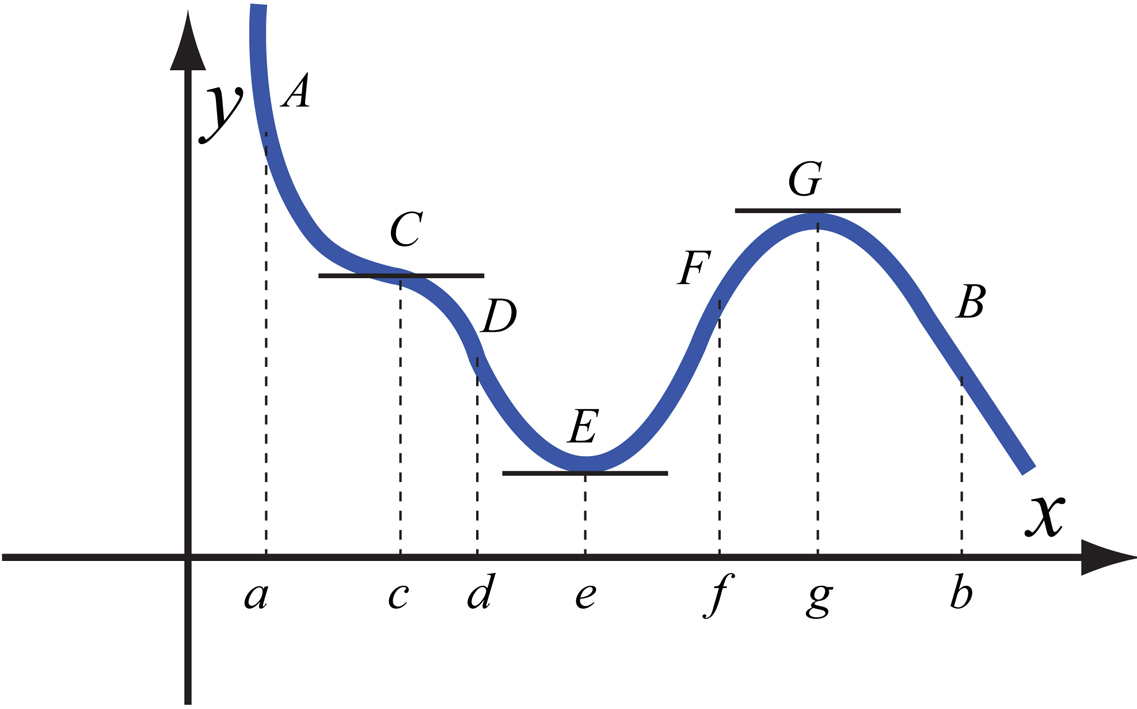
Вообичаено е локалниот ектрем да се нарекува само екстрем , затоа понатаму под поимот екстем ќе се подразбира локален екстрем.
Во делот Основни теореми на диференцијалното сметање , со теоремата на Ферма е даден потребниот услов за постоење на екстрем во точката , а тоа е таа да биде стационарна точка, односно . Секоја стацинорна точка не мора да биде точка на ектрем, тоа е потребен услов, а доволниот услов за екстем може да се спроведе преку две постапки:
Оваа постапка го користи знакот на првиот извод за утврдување на монотоноста на функцијата на интервал, а се базира на теоремата Лагранж.
За монотоноста (растењето и опаѓањето) на функцијата на итервалот ако важи:
, функцијата е строго монотоно растечка;
, функцијата е строго монотоно опаѓачка.
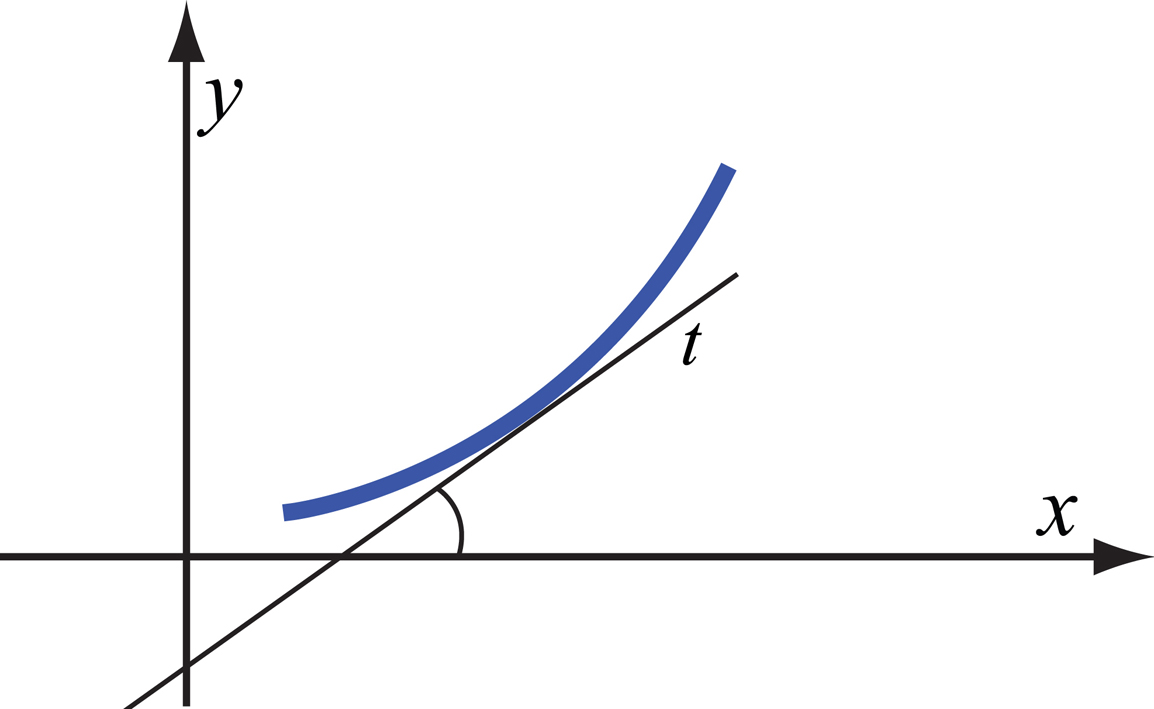
Навистина, ако на интервалот функцијата расте, тогаш и . Од теоремата на Лагранж следува дека постои точка за која ќе важи . Бидејќи функцијата е растечка, знакот на ќе биде ист со знакот на разликата , т.е. знакот е позитивен и затоа кога функцијата расте (Сл. 2.).
Со аналогна постапка се покажува дека ако , функцијата опаѓа (Сл. 3.).
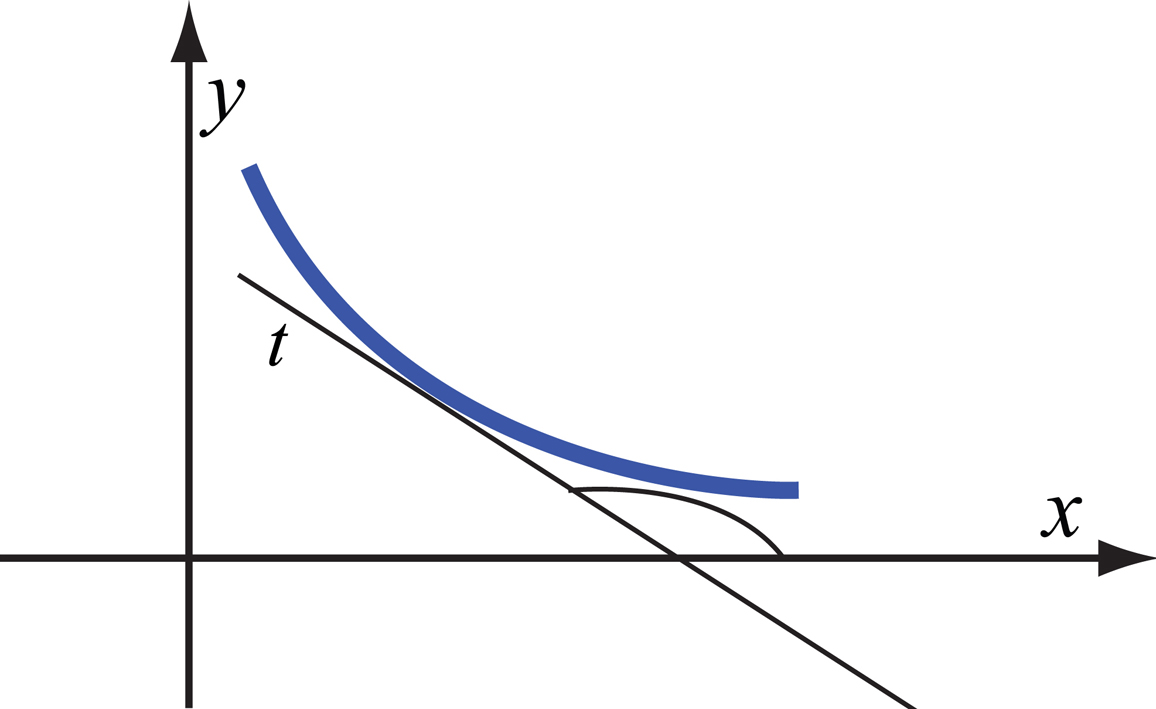
Овој факт ќе се примени во постапка за испитување на екстреми на функција преку знакот првиот извод и таа постапка се одвива во следните чекори:
1. Со решавање на равенката по се добиваат стационарните точки.
2. Секоја стационарна точка се подредува по својата вредност на бројната оска и со нив дефиниционата област се раздробува на таканаречени интервали на монотоност . Во секој од овие интервали изводната функцијата има постојан знак.

Notification Switch
Would you like to follow the 'Математика 1' conversation and receive update notifications?