3.1 Solving trigonometric equations with identities (Page 3/9)

Essential precalculus, part 2 Page 3 / 9

Reciprocal Identities
$\sin θ = \frac{1}{\csc θ}$	$\csc θ = \frac{1}{\sin θ}$
$\cos θ = \frac{1}{\sec θ}$	$\sec θ = \frac{1}{\cos θ}$
$\tan θ = \frac{1}{\cot θ}$	$\cot θ = \frac{1}{\tan θ}$

The final set of identities is the set of quotient identities , which define relationships among certain trigonometric functions and can be very helpful in verifying other identities. See [link] .


Quotient Identities
$\tan θ = \frac{\sin θ}{\cos θ}$	$\cot θ = \frac{\cos θ}{\sin θ}$

The reciprocal and quotient identities are derived from the definitions of the basic trigonometric functions.

A General Note

Summarizing trigonometric identities

The Pythagorean identities are based on the properties of a right triangle.

\cos^{2} θ + \sin^{2} θ = 1

1 + \cot^{2} θ = \csc^{2} θ

1 + \tan^{2} θ = \sec^{2} θ

The even-odd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle.

\tan (- θ) = - \tan θ

\cot (- θ) = - \cot θ

\sin (- θ) = - \sin θ

\csc (- θ) = - \csc θ

\cos (- θ) = \cos θ

\sec (- θ) = \sec θ

The reciprocal identities define reciprocals of the trigonometric functions.

\sin θ = \frac{1}{\csc θ}

\cos θ = \frac{1}{\sec θ}

\tan θ = \frac{1}{\cot θ}

\csc θ = \frac{1}{\sin θ}

\sec θ = \frac{1}{\cos θ}

\cot θ = \frac{1}{\tan θ}

The quotient identities define the relationship among the trigonometric functions.

\tan θ = \frac{\sin θ}{\cos θ}

\cot θ = \frac{\cos θ}{\sin θ}

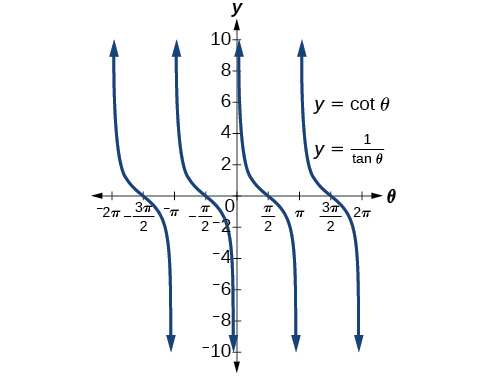
Graphing the equations of an identity

Graph both sides of the identity $\cot θ = \frac{1}{\tan θ} .$ In other words, on the graphing calculator, graph $y = \cot θ$ and $y = \frac{1}{\tan θ} .$

See [link] .

Graph of y = cot(theta) and y=1/tan(theta) from -2pi to 2pi. They are the same!

How To

Given a trigonometric identity, verify that it is true.

Work on one side of the equation. It is usually better to start with the more complex side, as it is easier to simplify than to build.
Look for opportunities to factor expressions, square a binomial, or add fractions.
Noting which functions are in the final expression, look for opportunities to use the identities and make the proper substitutions.
If these steps do not yield the desired result, try converting all terms to sines and cosines.

Verifying a trigonometric identity

Verify $\tan θ \cos θ = \sin θ .$

We will start on the left side, as it is the more complicated side:

\begin{array}{l} \tan θ \cos θ = (\frac{\sin θ}{\cos θ}) \cos θ \\ = (\frac{\sin θ}{\cos θ}) \cos θ \\ = \sin θ \end{array}

Try It

Verify the identity $\csc θ \cos θ \tan θ = 1.$

\begin{array}{l} \csc θ \cos θ \tan θ = (\frac{1}{\sin θ}) \cos θ (\frac{\sin θ}{\cos θ}) \\ = \frac{\cos θ}{\sin θ} (\frac{\sin θ}{\cos θ}) \\ = \frac{\sin θ \cos θ}{\sin θ \cos θ} \\ = 1 \end{array}

Verifying the equivalency using the even-odd identities

Verify the following equivalency using the even-odd identities:

(1 + \sin x) [1 + \sin (- x)] = \cos^{2} x

Working on the left side of the equation, we have

\begin{array}{l} (1 + \sin x) [1 + \sin (- x)] = (1 + \sin x) (1 - \sin x) & Since sin(− x)= - \sin x \\ = 1 - \sin^{2} x & Difference of squares \\ = \cos^{2} x & {cos}^{2} x = 1 - \sin^{2} x \end{array}

Verifying a trigonometric identity involving sec ² θ

Verify the identity $\frac{\sec^{2} θ - 1}{\sec^{2} θ} = \sin^{2} θ$

As the left side is more complicated, let’s begin there.

\begin{array}{l} \frac{\sec^{2} θ - 1}{\sec^{2} θ} = \frac{(\tan^{2} θ + 1) - 1}{\sec^{2} θ} & {sec}^{2} θ = \tan^{2} θ + 1 \\ = \frac{\tan^{2} θ}{\sec^{2} θ} \\ = \tan^{2} θ (\frac{1}{\sec^{2} θ}) \\ = \tan^{2} θ (\cos^{2} θ) & \cos^{2} θ = \frac{1}{\sec^{2} θ} \\ = (\frac{\sin^{2} θ}{\cos^{2} θ}) (\cos^{2} θ) & \begin{matrix} \begin{matrix}  \end{matrix} \end{matrix} & {tan}^{2} θ = \frac{\sin^{2} θ}{\cos^{2} θ} \\ = (\frac{\sin^{2} θ}{\cos^{2} θ}) (\cos^{2} θ) \\ = \sin^{2} θ \end{array}

There is more than one way to verify an identity. Here is another possibility. Again, we can start with the left side.

\begin{array}{l} \frac{\sec^{2} θ - 1}{\sec^{2} θ} = \frac{\sec^{2} θ}{\sec^{2} θ} - \frac{1}{\sec^{2} θ} \\ = 1 - \cos^{2} θ \\ = \sin^{2} θ \end{array}

<< Chapter < Page Page > Chapter >>

Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Essential precalculus, part 2. OpenStax CNX. Aug 20, 2015 Download for free at http://legacy.cnx.org/content/col11845/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?

Ask

	NCE Ch 03 Human Growth and Develoment By Anh Dao Start Test
	Classical Music By Marion Cabalfin Start Quiz
	33 Biology 33 The Animal Body Basic Form Function By OpenStax Start Quiz
	9 Biology 09 Cell Communication MCQ By OpenStax Start Quiz
	Clinical Issues in TB Management By Cath Yu Start Quiz
	5 Psychology MCQ 2010 1 Exam By John Gabrieli Start Exam
	8 Java Persistence API By JavaChamp Team Start Quiz
	Autonomic Nervous System By Marriyam Rana Start Quiz
	3 AP 03 Cellular Level of Organization MCQ By OpenStax Start Quiz
	7 Neuroanatomy 07 The Visual System By Stephen Voron Start Quiz