3.1 Discrete-time fourier transform (dtft)

Ece 454 and ece 554 supplemental Page 1 / 1

Discussion of Discrete-time Fourier Transforms. Topics include comparison with analog transforms and discussion of Parseval's theorem.

The Fourier transform of the discrete-time signal $s n$ is defined to be

S 2 f n

∞ ∞ s n 2 f n

Frequency here has no units. As should be expected, thisdefinition is linear, with the transform of a sum of signals equaling the sum of their transforms. Real-valued signals haveconjugate-symmetric spectra:

S 2 f S j 2 f

A special property of the discrete-time Fourier transform isthat it is periodic with period one: $S 2 f 1 S 2 f$ . Derive this property from the definition of the DTFT.

S 2 f 1 n

∞ ∞ s n 2 f 1 n n ∞ ∞ 2 n s n 2 f n n ∞ ∞ s n 2 f n S 2 f

Because of this periodicity, we need only plot the spectrum overone period to understand completely the spectrum's structure; typically, we plot the spectrum over the frequency range $1212$ . When the signal is real-valued, we can further simplify ourplotting chores by showing the spectrum only over $012$ ; the spectrum at negative frequencies can be derived frompositive-frequency spectral values.

When we obtain the discrete-time signal via sampling an analog signal, the Nyquist frequency corresponds to the discrete-time frequency $12$ . To show this, note that a sinusoid having a frequency equal to the Nyquist frequency $1 2 T_{s}$ has a sampled waveform that equals $2 1 2 T s n T s n 1 n$ The exponential in the DTFT at frequency $12$ equals $2 n 2 n 1 n$ , meaning that discrete-time frequency equals analog frequency multiplied by the sampling interval

f_{D} f_{A} T_{s}

f_{D}

and

f_{A}

represent discrete-time and analog frequency variables, respectively. The aliasing figure provides another way of deriving this result. As the duration of eachpulse in the periodic sampling signal

p_{T_{s}} t

narrows, the amplitudes of the signal's spectral repetitions, which are governed by the Fourier series coefficients of

p_{T_{s}} t

, become increasingly equal. Examination of the periodic pulse signal reveals that as

Δ

decreases, the value of

c_{0}

, the largest Fourier coefficient, decreases to zero:

c_{0} A Δ T_{s}

. Thus, to maintain a mathematically viable Sampling Theorem, theamplitude

A

must increase as

1 Δ

, becoming infinitely large as the pulse duration decreases. Practical systems use a small value of

Δ

, say

0.1 · T_{s}

and use amplifiers to rescale the signal. Thus, the sampledsignal's spectrum becomes periodic with period

1 T_{s}

. Thus, the Nyquist frequency

1 2 T_{s}

corresponds to the frequency

12

Let's compute the discrete-time Fourier transform of the exponentially decaying sequence $s n a n u n$ , where $u n$ is the unit-step sequence. Simply plugging the signal'sexpression into the Fourier transform formula,

S 2 f n

∞ ∞ a n u n 2 f n n ∞ 0 a 2 f n

This sum is a special case of the geometric series .

n 0

∞ α n α α 1 1 1 α

Thus, as long as $a 1$ , we have our Fourier transform.

S 2 f 1 1 a 2 f

Using Euler's relation, we can express the magnitude and phase of this spectrum.

S 2 f 1 1 a 2 f 2 a 2 2 f 2

S 2 f a 2 f 1 a 2 f

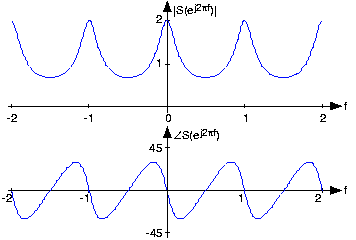
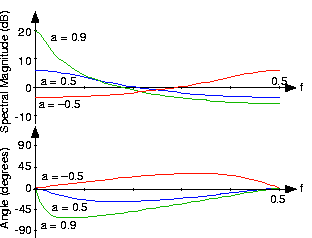
No matter what value of $a$ we choose, the above formulae clearly demonstrate the periodicnature of the spectra of discrete-time signals. [link] shows indeed that the spectrum is a periodic function. We need only consider the spectrumbetween $12$ and $12$ to unambiguously define it. When $a 0$ , we have a lowpass spectrum—the spectrum diminishes asfrequency increases from 0 to $12$ —with increasing $a$ leading to a greater low frequency content; for $a 0$ , we have a highpass spectrum( [link] ).

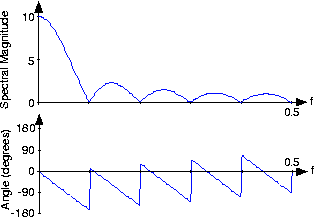
The spectrum of the exponential signal ( $a 0.5$ ) is shown over the frequency range [-2, 2], clearly demonstrating the periodicity of all discrete-time spectra. The angle has unitsof degrees.

The spectra of several exponential signals are shown. What is the apparent relationship between the spectra for $a 0.5$ and $a 0.5$ ?

Analogous to the analog pulse signal, let's find the spectrum of the length- $N$ pulse sequence.

s n 1 0 n N 1 0

The Fourier transform of this sequence has the form of a truncated geometric series.

S 2 f n 0 N 1 2 f n

For the so-called finite geometric series, we know that

n n_{0} N n_{0} 1 α n α n_{0} 1 α N 1 α

for all values of α.

Derive this formula for the finite geometric series sum. The "trick" is to consider the difference between theseries' sum and the sum of the series multiplied by $α$ .

$α n n_{0} N n_{0} 1 α n n n_{0} N n_{0} 1 α n α N n_{0} α n_{0}$ which, after manipulation, yields the geometric sum formula.

Applying this result yields ( [link] .)

S 2 f 1 2 f N 1 2 f f N 1 f N f

The ratio of sine functions has the generic form of

N x x

, which is known as the discrete-time sinc function

dsinc x

. Thus, our transform can be concisely expressed as

S 2 f f N 1 dsinc f

. The discrete-time pulse's spectrum contains many ripples, the number of which increase with

N

, the pulse's duration.

The spectrum of a length-ten pulse is shown. Can you explain the rather complicated appearance of the phase?

The inverse discrete-time Fourier transform is easily derived from the following relationship:

1212 f 2 f m 2 f n 1 m n 0 m n δ m n

Therefore, we find that

f 1212 S 2 f 2 f n f 1212 m m s m 2 f m 2 f n m m s m f 1212 2 f m n s n

The Fourier transform pairs in discrete-time are

\begin{array}{l} S 2 f n \end{array}

∞ ∞ s n 2 f n s n f 1 2 1 2 S 2 f 2 f n

The properties of the discrete-time Fourier transform mirror those of the analog Fourier transform. The DTFT properties table shows similarities and differences. One important common property is Parseval's Theorem.

n

∞ ∞ s n 2 f 1 2 1 2 S 2 f 2

To show this important property, we simply substitute theFourier transform expression into the frequency-domain expression for power.

f 1212 S 2 f 2 f 1212 n n s n 2 f n m m s n 2 f m, n m, n m s n s n f 1212 2 f m n

Using the orthogonality relation , the integral equals

δ m n

, where

δ n

is the unit sample . Thus, the double sum collapses into a single sum because nonzero values occur only when

n m

, giving Parseval's Theorem as a result. We term

n n s n 2

the energy in the discrete-time signal

s n

in spite of the fact that discrete-time signals don't consume(or produce for that matter) energy. This terminology is a carry-over from the analog world.

Suppose we obtained our discrete-time signal from values ofthe product $s t p_{T_{s}} t$ , where the duration of the component pulses in $p_{T_{s}} t$ is $Δ$ . How is the discrete-time signal energy related to the total energycontained in $s t$ ? Assume the signal is bandlimited and that the sampling ratewas chosen appropriate to the Sampling Theorem's conditions.

If the sampling frequency exceeds the Nyquist frequency, thespectrum of the samples equals the analog spectrum, but overthe normalized analog frequency $f T$ . Thus, the energy in the sampled signal equals the original signal's energy multiplied by $T$ .

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Ece 454 and ece 554 supplemental reading. OpenStax CNX. Apr 02, 2012 Download for free at http://cnx.org/content/col11416/1.1

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Ece 454 and ece 554 supplemental reading' conversation and receive update notifications?

Ask

	Corporate Communication BUS210 By P. Wynn Norman Start Quiz
	Are you part of the R5 Family? By Anonymous User Start Quiz
	17 Dr. Avery GI Bio Path quiz By Brooke Delaney Start Exam
	Grade 10 Module 2.1 IT Quiz (Part 1) By Christine Zeelie Start Quiz
	5 Sociology 05 Socialization MCQ By OpenStax Start Quiz
©flickr: U.S.	Biology Chapter 9 By Michael Sag Start Exam
	34 Biology 34 Animal Nutrition Digestive System By OpenStax Start Quiz
©flickr:	The Minute Man Hose Load By Michael Pitt Start Quiz
	Anthropology Religion Culture By Richley Crapo Start Assignment
	6 AP 06 Skeletal System MCQ By OpenStax Start Quiz

3.1 Discrete-time fourier transform (dtft)

Spectrum of exponential signal

Spectra of exponential signals

Spectrum of length-ten pulse

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!