3.1 Current  (Page 4/8)

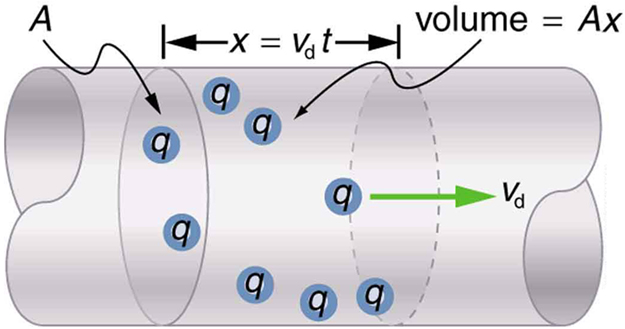
We can obtain an expression for the relationship between current and drift velocity by considering the number of free charges in a segment of wire, as illustrated in [link] . The number of free charges per unit volume is given the symbol $n$ and depends on the material. The shaded segment has a volume $\text{Ax}$ , so that the number of free charges in it is $\text{nAx}$ . The charge $\mathrm{\Delta }Q$ in this segment is thus $\text{qnAx}$ , where $q$ is the amount of charge on each carrier. (Recall that for electrons, $q$ is $-1\text{.}\text{60}\times {\text{10}}^{-\text{19}}\text{C}$ .) Current is charge moved per unit time; thus, if all the original charges move out of this segment in time $\mathrm{\Delta }t$ , the current is

Note that $x/\mathrm{\Delta }t$ is the magnitude of the drift velocity, $v_{\text{d}}$ , since the charges move an average distance $x$ in a time $\mathrm{\Delta }t$ . Rearranging terms gives

where $I$ is the current through a wire of cross-sectional area $A$ made of a material with a free charge density $n$ . The carriers of the current each have charge $q$ and move with a drift velocity of magnitude $v_{\text{d}}$ .

Note that simple drift velocity is not the entire story. The speed of an electron is much greater than its drift velocity. In addition, not all of the electrons in a conductor can move freely, and those that do might move somewhat faster or slower than the drift velocity. So what do we mean by free electrons? Atoms in a metallic conductor are packed in the form of a lattice structure. Some electrons are far enough away from the atomic nuclei that they do not experience the attraction of the nuclei as much as the inner electrons do. These are the free electrons. They are not bound to a single atom but can instead move freely among the atoms in a “sea” of electrons. These free electrons respond by accelerating when an electric field is applied. Of course as they move they collide with the atoms in the lattice and other electrons, generating thermal energy, and the conductor gets warmer. In an insulator, the organization of the atoms and the structure do not allow for such free electrons.