| << Chapter < Page | Chapter >> Page > |
Calculate the following derivatives:
We need to apply the chain rule in both cases.
Note that if we use the absolute value function and create a new function we can extend the domain of the natural logarithm to include Then This gives rise to the familiar integration formula.
The natural logarithm is the antiderivative of the function
Calculate the integral
Using -substitution, let Then and we have
Although we have called our function a “logarithm,” we have not actually proved that any of the properties of logarithms hold for this function. We do so here.
If and is a rational number, then
□
Use properties of logarithms to simplify the following expression into a single logarithm:
We have
Use properties of logarithms to simplify the following expression into a single logarithm:
Now that we have the natural logarithm defined, we can use that function to define the number
The number is defined to be the real number such that
To put it another way, the area under the curve between and is ( [link] ). The proof that such a number exists and is unique is left to you. ( Hint : Use the Intermediate Value Theorem to prove existence and the fact that is increasing to prove uniqueness.)
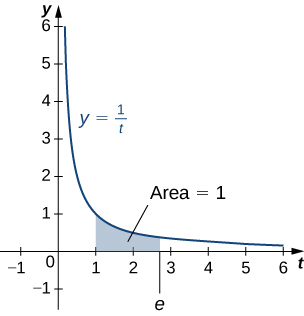
The number can be shown to be irrational, although we won’t do so here (see the Student Project in Taylor and Maclaurin Series ). Its approximate value is given by
We now turn our attention to the function Note that the natural logarithm is one-to-one and therefore has an inverse function. For now, we denote this inverse function by Then,

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?