| << Chapter < Page | Chapter >> Page > |
Let’s now apply this definition to calculate a differentiation formula for We have
The corresponding integration formula follows immediately.
Let Then,
and
If then the function is one-to-one and has a well-defined inverse. Its inverse is denoted by Then,
Note that general logarithm functions can be written in terms of the natural logarithm. Let Then, Taking the natural logarithm of both sides of this second equation, we get
Thus, we see that all logarithmic functions are constant multiples of one another. Next, we use this formula to find a differentiation formula for a logarithm with base Again, let Then,
Let Then,
Evaluate the following derivatives:
We need to apply the chain rule as necessary.
Evaluate the following integral:
Use and let Then and we have
For the following exercises, find the derivative
For the following exercises, find the indefinite integral.
For the following exercises, find the derivative (You can use a calculator to plot the function and the derivative to confirm that it is correct.)
For the following exercises, find the definite or indefinite integral.
For the following exercises, compute by differentiating
For the following exercises, evaluate by any method.
For the following exercises, use the function If you are unable to find intersection points analytically, use a calculator.
[T] Find the arc length of from to
Find the volume of the shape created when rotating this curve from around the x -axis, as pictured here.
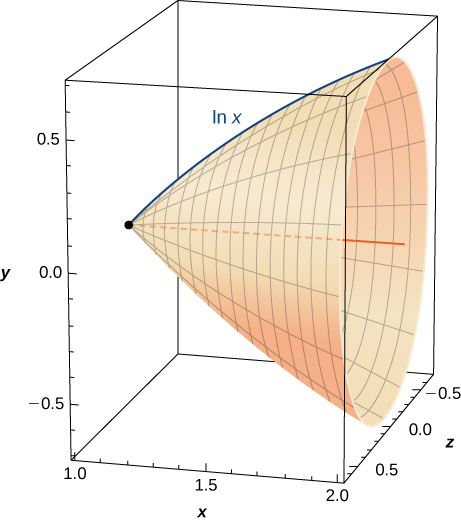
[T] Find the surface area of the shape created when rotating the curve in the previous exercise from to around the x -axis.
If you are unable to find intersection points analytically in the following exercises, use a calculator.
Find the area of the hyperbolic quarter-circle enclosed by above
Find the area under and above the x -axis from
For the following exercises, verify the derivatives and antiderivatives.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?