2.5 Capacitors and dielectrics  (Page 2/12)

This equation expresses the two major factors affecting the amount of charge stored. Those factors are the physical characteristics of the capacitor, $C$ , and the voltage, $V$ . Rearranging the equation, we see that capacitance $C$ is the amount of charge stored per volt, or

The unit of capacitance is the farad (F), named for Michael Faraday (1791–1867), an English scientist who contributed to the fields of electromagnetism and electrochemistry. Since capacitance is charge per unit voltage, we see that a farad is a coulomb per volt, or

A 1-farad capacitor would be able to store 1 coulomb (a very large amount of charge) with the application of only 1 volt. One farad is, thus, a very large capacitance. Typical capacitors range from fractions of a picofarad $\left(\mathrm{1\; pF}={\text{10}}^{\text{–12}}\text{F}\right)$ to millifarads $\left(\mathrm{1\; mF}={\text{10}}^{\mathrm{–3}}\text{F}\right)$ .

[link] shows some common capacitors. Capacitors are primarily made of ceramic, glass, or plastic, depending upon purpose and size. Insulating materials, called dielectrics, are commonly used in their construction, as discussed below.

Parallel plate capacitor

The parallel plate capacitor shown in [link] has two identical conducting plates, each having a surface area $A$ , separated by a distance $d$ (with no material between the plates). When a voltage $V$ is applied to the capacitor, it stores a charge $Q$ , as shown. We can see how its capacitance depends on $A$ and $d$ by considering the characteristics of the Coulomb force. We know that like charges repel, unlike charges attract, and the force between charges decreases with distance. So it seems quite reasonable that the bigger the plates are, the more charge they can store—because the charges can spread out more. Thus $C$ should be greater for larger $A$ . Similarly, the closer the plates are together, the greater the attraction of the opposite charges on them. So $C$ should be greater for smaller $d$ .

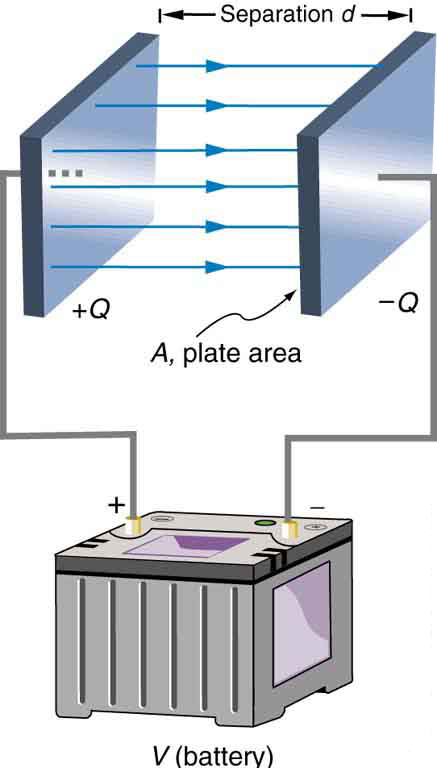
It can be shown that for a parallel plate capacitor there are only two factors ( $A$ and $d$ ) that affect its capacitance $C$ . The capacitance of a parallel plate capacitor in equation form is given by

$A$ is the area of one plate in square meters, and $d$ is the distance between the plates in meters. The constant ${\epsilon }_0$ is the permittivity of free space; its numerical value in SI units is ${\epsilon }_0=8.85\times {\text{10}}^{–\text{12}}\text{F/m}$ . The units of F/m are equivalent to ${\mathrm{C}}^2\text{/N}·{\text{m}}^2$ . The small numerical value of ${\epsilon }_0$ is related to the large size of the farad. A parallel plate capacitor must have a large area to have a capacitance approaching a farad. (Note that the above equation is valid when the parallel plates are separated by air or free space. When another material is placed between the plates, the equation is modified, as discussed below.)