2.2 Electric potential in a uniform electric field  (Page 8/5)

In the previous section, we explored the relationship between voltage and energy. In this section, we will explore the relationship between voltage and electric field. For example, a uniform electric field $\mathbf{\text{E}}$ is produced by placing a potential difference (or voltage) $\mathrm{\Delta }V$ across two parallel metal plates, labeled A and B. (See [link] .) Examining this will tell us what voltage is needed to produce a certain electric field strength; it will also reveal a more fundamental relationship between electric potential and electric field. From a physicist’s point of view, either $\mathrm{\Delta }V$ or $\mathbf{\text{E}}$ can be used to describe any charge distribution. $\mathrm{\Delta }V$ is most closely tied to energy, whereas $\mathbf{\text{E}}$ is most closely related to force. $\mathrm{\Delta }V$ is a scalar    quantity and has no direction, while $\mathbf{\text{E}}$ is a vector    quantity, having both magnitude and direction. (Note that the magnitude of the electric field strength, a scalar quantity, is represented by $E$ below.) The relationship between $\mathrm{\Delta }V$ and $\mathbf{\text{E}}$ is revealed by calculating the work done by the force in moving a charge from point A to point B. But, as noted in Electric Potential Energy: Potential Difference , this is complex for arbitrary charge distributions, requiring calculus. We therefore look at a uniform electric field as an interesting special case.

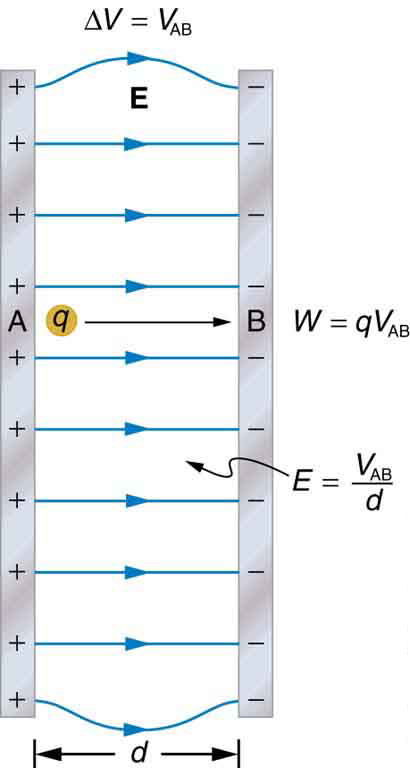
The work done by the electric field in [link] to move a positive charge $q$ from A, the positive plate, higher potential, to B, the negative plate, lower potential, is

The potential difference between points A and B is

Entering this into the expression for work yields

Work is $W=\text{Fd}\text{cos}\theta$ ; here $\text{cos}\theta =1$ , since the path is parallel to the field, and so $W=\text{Fd}$ . Since $F=\text{qE}$ , we see that $W=\text{qEd}$ . Substituting this expression for work into the previous equation gives

The charge cancels, and so the voltage between points A and B is seen to be

where $d$ is the distance from A to B, or the distance between the plates in [link] . Note that the above equation implies the units for electric field are volts per meter. We already know the units for electric field are newtons per coulomb; thus the following relation among units is valid: