1. Home
  2. Une: physics for the health
  3. Extras
  4. Elasticity: stress and strain

13.2 Elasticity: stress and strain  (Page 6/15)

<< Chapter < Page
  Une: physics for the health     Page 6 / 15
Chapter >> Page >

Calculating force required to deform: that nail does not bend much under a load

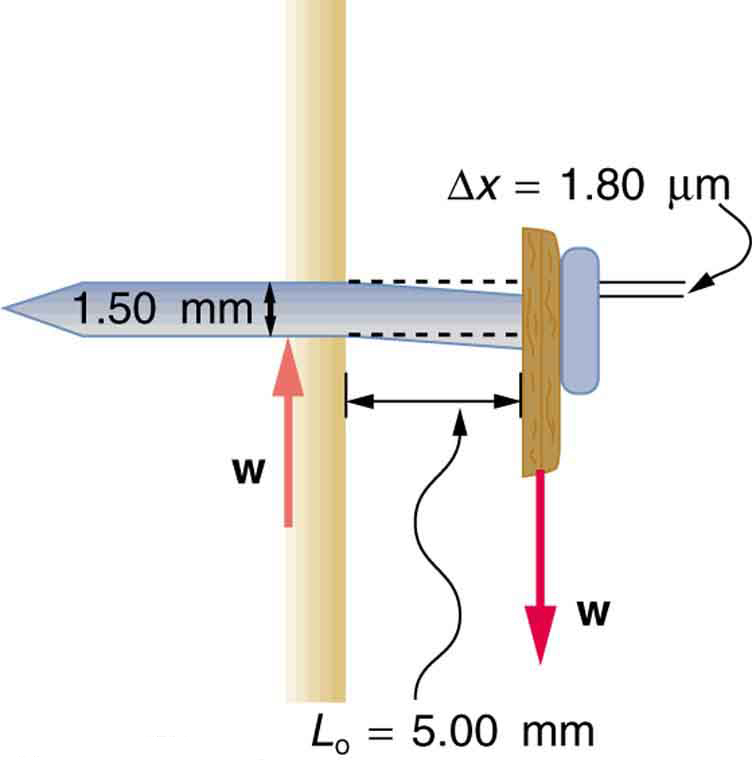
Find the mass of the picture hanging from a steel nail as shown in [link] , given that the nail bends only 1.80 µm size 12{ left (1 "." "80" times "10" rSup { size 8{ - 6} } m right )} {} . (Assume the shear modulus is known to two significant figures.)

Diagram showing the side view a nail in a wall, deformed by the weight of a picture hanging from it. The weight w of the picture is downward. There is an equal force w upward on the nail from the wall. The nail is 1 point five zero millimeters thick. The length of the nail that is outside the wall is five point zero zero millimeters. The deformation delta x of the nail as a result of the picture is 1 point eight zero micrometers.
Side view of a nail with a picture hung from it. The nail flexes very slightly (shown much larger than actual) because of the shearing effect of the supported weight. Also shown is the upward force of the wall on the nail, illustrating that there are equal and opposite forces applied across opposite cross sections of the nail. See [link] for a calculation of the mass of the picture.

Strategy

The force F size 12{F} {} on the nail (neglecting the nail’s own weight) is the weight of the picture w size 12{w} {} . If we can find w size 12{w} {} , then the mass of the picture is just w g size 12{ { {w} over {g} } } {} . The equation Δ x = 1 S F A L 0 size 12{Δx= { {1} over {S} } { {F} over {A} } L rSub { size 8{0} } } {} can be solved for F size 12{F} {} .

Solution

Solving the equation Δ x = 1 S F A L 0 size 12{Δx= { {1} over {S} } { {F} over {A} } L rSub { size 8{0} } } {} for F , we see that all other quantities can be found:

F = SA L 0 Δ x . size 12{F= { { ital "SA"} over {L rSub { size 8{0} } } } Δx} {}

S is found in [link] and is S = 80 × 10 9 N/m 2 size 12{S="80" times "10" rSup { size 8{9} } " N/m" rSup { size 8{2} } } {} . The radius r size 12{r} {} is 0.750 mm (as seen in the figure), so the cross-sectional area is

A = πr 2 = 1 . 77 × 10 − 6 m 2 . size 12{A=πr rSup { size 8{2} } =1 "." "77" times "10" rSup { size 8{ - 6} } m rSup { size 8{2} } } {}

The value for L 0 size 12{L rSub { size 8{0} } } {} is also shown in the figure. Thus,

F = ( 80 × 10 9 N/m 2 ) ( 1 . 77 × 10 − 6 m 2 ) ( 5 . 00 × 10 − 3 m ) ( 1 . 80 × 10 − 6 m ) = 51 N. size 12{F= { { \( "80" times "10" rSup { size 8{9} } " N/m" rSup { size 8{2} } \) \( 1 "." "77" times "10" rSup { size 8{ - 6} } " m" rSup { size 8{2} } \) } over { \( 5 "." "00" times "10" rSup { size 8{ - 3} } " m" \) } } times \( 1 "." "80" times "10" rSup { size 8{ - 6} } " m" \) ="51"N} {}

This 51 N force is the weight w of the picture, so the picture’s mass is

m = w g = F g = 5 .2 kg . size 12{m= { {w} over {g} } = { {F} over {g} } =5 "." 2" kg"} {}

Discussion

This is a fairly massive picture, and it is impressive that the nail flexes only 1.80 µm —an amount undetectable to the unaided eye.

Changes in volume: bulk modulus

An object will be compressed in all directions if inward forces are applied evenly on all its surfaces as in [link] . It is relatively easy to compress gases and extremely difficult to compress liquids and solids. For example, air in a wine bottle is compressed when it is corked. But if you try corking a brim-full bottle, you cannot compress the wine—some must be removed if the cork is to be inserted. The reason for these different compressibilities is that atoms and molecules are separated by large empty spaces in gases but packed close together in liquids and solids. To compress a gas, you must force its atoms and molecules closer together. To compress liquids and solids, you must actually compress their atoms and molecules, and very strong electromagnetic forces in them oppose this compression.

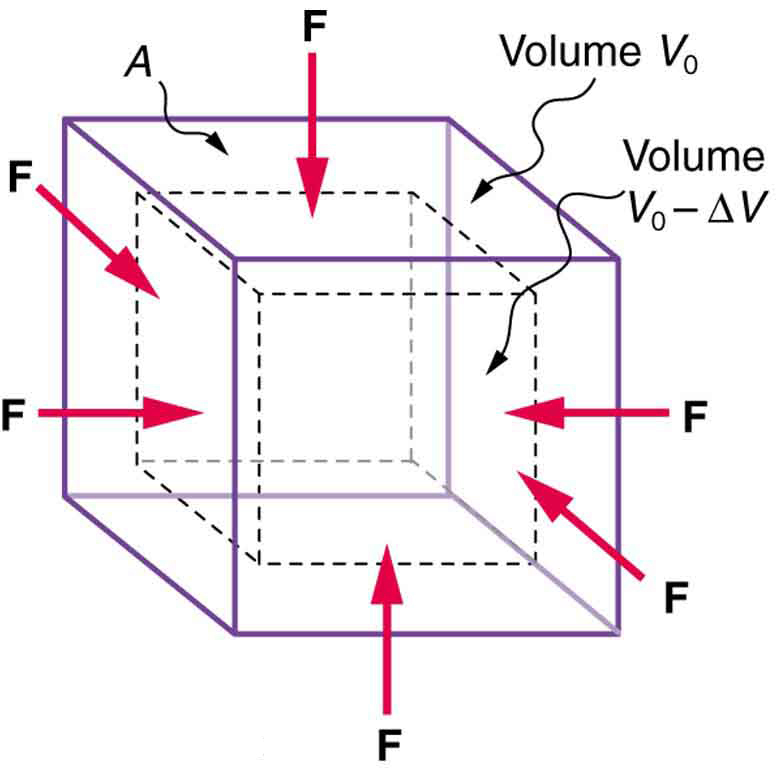
A cube with area of cross section A and volume V zero is compressed by an inward force F acting on all surfaces. The compression causes a change in volume delta V, which is proportional to the force per unit area and its original volume. This change in volume is related to the compressibility of the substance.
An inward force on all surfaces compresses this cube. Its change in volume is proportional to the force per unit area and its original volume, and is related to the compressibility of the substance.

We can describe the compression or volume deformation of an object with an equation. First, we note that a force “applied evenly” is defined to have the same stress, or ratio of force to area F A size 12{ left ( { {F} over {A} } right )} {} on all surfaces. The deformation produced is a change in volume Δ V size 12{ΔV} {} , which is found to behave very similarly to the shear, tension, and compression previously discussed. (This is not surprising, since a compression of the entire object is equivalent to compressing each of its three dimensions.) The relationship of the change in volume to other physical quantities is given by

Δ V = 1 B F A V 0 , size 12{ΔV= { {1} over {B} } { {F} over {A} } V rSub { size 8{0} } } {}
<< Chapter < Page Page > Chapter >>
Practice Key Terms 6

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Une: physics for the health professions. OpenStax CNX. Aug 20, 2014 Download for free at http://legacy.cnx.org/content/col11697/1.1
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Une: physics for the health professions' conversation and receive update notifications?

Ask