13.2 Elasticity: stress and strain  (Page 3/15)

The stretch of a long cable

Suspension cables are used to carry gondolas at ski resorts. (See [link] ) Consider a suspension cable that includes an unsupported span of 3 km. Calculate the amount of stretch in the steel cable. Assume that the cable has a diameter of 5.6 cm and the maximum tension it can withstand is $3\text{.}0\times {\text{10}}^6\text{N}$ .

Strategy

The force is equal to the maximum tension, or $F=3\text{.}0\times {\text{10}}^6\text{N}$ . The cross-sectional area is ${\mathrm{\pi r}}^2=2\text{.}\text{46}\times {\text{10}}^{-3}{\text{m}}^2$ . The equation $\mathrm{\Delta }L=\frac{1}{Y}\frac{F}{A}{L}_0$ can be used to find the change in length.

Solution

All quantities are known. Thus,

$\begin{array}{lll}\mathrm{\Delta }L& =& \left(\frac{1}{\text{210}\times {\text{10}}^9{\text{N/m}}^2}\right)\left(\frac{3\text{.}0\times {\text{10}}^6\text{N}}{2.46\times {10}^{\mathrm{–3}}{\text{m}}^2}\right)\left(\text{3020 m}\right)\\ & =& \text{18 m}.\end{array}$

Discussion

This is quite a stretch, but only about 0.6% of the unsupported length. Effects of temperature upon length might be important in these environments.

Bones, on the whole, do not fracture due to tension or compression. Rather they generally fracture due to sideways impact or bending, resulting in the bone shearing or snapping. The behavior of bones under tension and compression is important because it determines the load the bones can carry. Bones are classified as weight-bearing structures such as columns in buildings and trees. Weight-bearing structures have special features; columns in building have steel-reinforcing rods while trees and bones are fibrous. The bones in different parts of the body serve different structural functions and are prone to different stresses. Thus the bone in the top of the femur is arranged in thin sheets separated by marrow while in other places the bones can be cylindrical and filled with marrow or just solid. Overweight people have a tendency toward bone damage due to sustained compressions in bone joints and tendons.

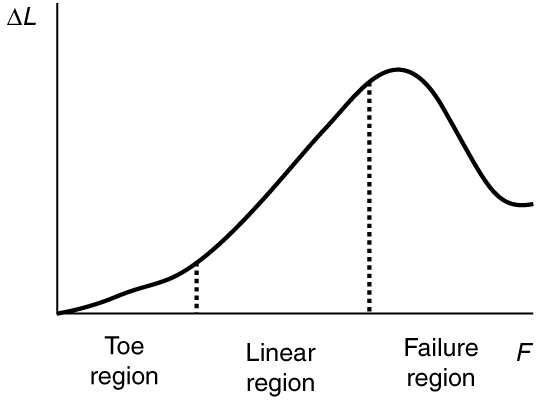
Another biological example of Hooke’s law occurs in tendons. Functionally, the tendon (the tissue connecting muscle to bone) must stretch easily at first when a force is applied, but offer a much greater restoring force for a greater strain. [link] shows a stress-strain relationship for a human tendon. Some tendons have a high collagen content so there is relatively little strain, or length change; others, like support tendons (as in the leg) can change length up to 10%. Note that this stress-strain curve is nonlinear, since the slope of the line changes in different regions. In the first part of the stretch called the toe region, the fibers in the tendon begin to align in the direction of the stress—this is called uncrimping . In the linear region, the fibrils will be stretched, and in the failure region individual fibers begin to break. A simple model of this relationship can be illustrated by springs in parallel: different springs are activated at different lengths of stretch. Examples of this are given in the problems at end of this chapter. Ligaments (tissue connecting bone to bone) behave in a similar way.