1. Home
  2. Collaborative statistics (with
  3. Appendix
  4. Practice final exam 2

13.1 Practice final exam 2  (Page 3/2)

<< Chapter < Page
  Collaborative statistics (with     Page 1 / 2
Chapter >> Page >
This module is a practice final for an associated elementary statistics textbook, Collaborative Statistics, available for Fall 2008.

A study was done to determine the proportion of teenagers that own a car. The population proportion of teenagers that own a car is the

  • statistic
  • parameter
  • population
  • variable

B: parameter

The next two questions refer to the following data:

value frequency
0 1
1 4
2 7
3 9
6 4

The box plot for the data is:

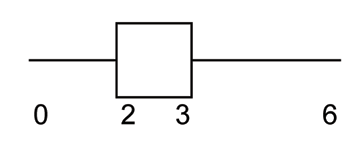
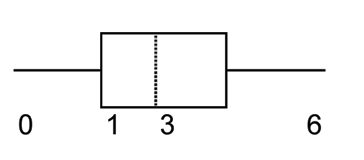
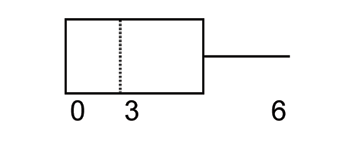
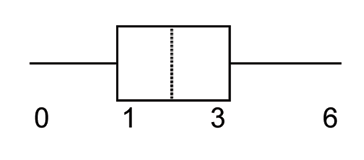
A

If 6 were added to each value of the data in the table, the 15th percentile of the new list of values is:

  • 6
  • 1
  • 7
  • 8

C: 7

The next two questions refer to the following situation:

Suppose that the probability of a drought in any independent year is 20%. Out of those years in which a drought occurs, the probability of water rationing is 10%. However, in any year, the probability of water rationing is 5%.

What is the probability of both a drought and water rationing occurring?

  • 0.05
  • 0.01
  • 0.02
  • 0.30

C: 0.02

Which of the following is true?

  • drought and water rationing are independent events
  • drought and water rationing are mutually exclusive events
  • none of the above

C: none of the above

The next two questions refer to the following situation:

Suppose that a survey yielded the following data:

Favorite pie type
gender apple pumpkin pecan
female 40 10 30
male 20 30 10

Suppose that one individual is randomly chosen. The probability that the person’s favorite pie is apple or the person is male is:

  • 40 60
  • 60 140
  • 120 140
  • 100 140

D: 100 140

Suppose H o is: Favorite pie type and gender are independent.

The p-value is:

  • ≈ 0
  • 1
  • 0.05
  • cannot be determined

A: ≈ 0

The next two questions refer to the following situation:

Let’s say that the probability that an adult watches the news at least once per week is 0.60. We randomly survey 14 people. Of interest is the number that watch the news at least once per week.

Which of the following statements is FALSE?

  • X ~ B 14 0.60
  • The values for x are: { 1 , 2 , 3 , ... , 14 }
  • μ = 8.4
  • P ( X = 5 ) = 0.0408

B: The values for x are: { 1 , 2 , 3 , ... , 14 }

Find the probability that at least 6 adults watch the news.

  • 6 14
  • 0.8499
  • 0.9417
  • 0.6429

C: 0.9417

The following histogram is most likely to be a result of sampling from which distribution?

  • Chi-Square with df = 6
  • Exponential
  • Uniform
  • Binomial

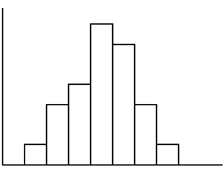
D: Binomial

The ages of campus day and evening students is known to be normally distributed. A sample of 6 campus day and evening students reported their ages (in years) as: { 18 , 35 , 27 , 45 , 20 , 20 }

What is the error bound for the 90% confidence interval of the true average age?

  • 11.2
  • 22.3
  • 17.5
  • 8.7

D: 8.7

If a normally distributed random variable has µ = 0 and σ = 1 , then 97.5% of the population values lie above:

  • -1.96
  • 1.96
  • 1
  • -1

A: -1.96

The next three questions refer to the following situation:

The amount of money a customer spends in one trip to the supermarket is known to have an exponential distribution. Suppose the average amount of money a customer spends in one trip to the supermarket is $72.

What is the probability that one customer spends less than $72 in one trip to the supermarket?

  • 0.6321
  • 0.5000
  • 0.3714
  • 1

A: 0.6321

How much money altogether would you expect next 5 customers to spend in one trip to the supermarket (in dollars)?

  • 72
  • 72 2 5
  • 5184
  • 360

D: 360

Questions & Answers

I'm interested in biological psychology and cognitive psychology
Tanya Reply
what does preconceived mean
sammie Reply
physiological Psychology
Nwosu Reply
How can I develope my cognitive domain
Amanyire Reply
why is communication effective
Dakolo Reply
Communication is effective because it allows individuals to share ideas, thoughts, and information with others.
effective communication can lead to improved outcomes in various settings, including personal relationships, business environments, and educational settings. By communicating effectively, individuals can negotiate effectively, solve problems collaboratively, and work towards common goals.
it starts up serve and return practice/assessments.it helps find voice talking therapy also assessments through relaxed conversation.
miss
Every time someone flushes a toilet in the apartment building, the person begins to jumb back automatically after hearing the flush, before the water temperature changes. Identify the types of learning, if it is classical conditioning identify the NS, UCS, CS and CR. If it is operant conditioning, identify the type of consequence positive reinforcement, negative reinforcement or punishment
Wekolamo Reply
please i need answer
Wekolamo
because it helps many people around the world to understand how to interact with other people and understand them well, for example at work (job).
Manix Reply
Agreed 👍 There are many parts of our brains and behaviors, we really need to get to know. Blessings for everyone and happy Sunday!
ARC
A child is a member of community not society elucidate ?
JESSY Reply
Isn't practices worldwide, be it psychology, be it science. isn't much just a false belief of control over something the mind cannot truly comprehend?
Simon Reply
compare and contrast skinner's perspective on personality development on freud
namakula Reply
Skinner skipped the whole unconscious phenomenon and rather emphasized on classical conditioning
war
explain how nature and nurture affect the development and later the productivity of an individual.
Amesalu Reply
nature is an hereditary factor while nurture is an environmental factor which constitute an individual personality. so if an individual's parent has a deviant behavior and was also brought up in an deviant environment, observation of the behavior and the inborn trait we make the individual deviant.
Samuel
I am taking this course because I am hoping that I could somehow learn more about my chosen field of interest and due to the fact that being a PsyD really ignites my passion as an individual the more I hope to learn about developing and literally explore the complexity of my critical thinking skills
Zyryn Reply
good👍
Jonathan
and having a good philosophy of the world is like a sandwich and a peanut butter 👍
Jonathan
generally amnesi how long yrs memory loss
Kelu Reply
interpersonal relationships
Abdulfatai Reply
What would be the best educational aid(s) for gifted kids/savants?
Heidi Reply
treat them normal, if they want help then give them. that will make everyone happy
Saurabh
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Collaborative statistics (with edits: teegarden). OpenStax CNX. Jul 20, 2009 Download for free at http://legacy.cnx.org/content/col10561/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Collaborative statistics (with edits: teegarden)' conversation and receive update notifications?

Ask