12.7 Ultrasound  (Page 5/10)

Calculate velocity of blood: doppler-shifted ultrasound

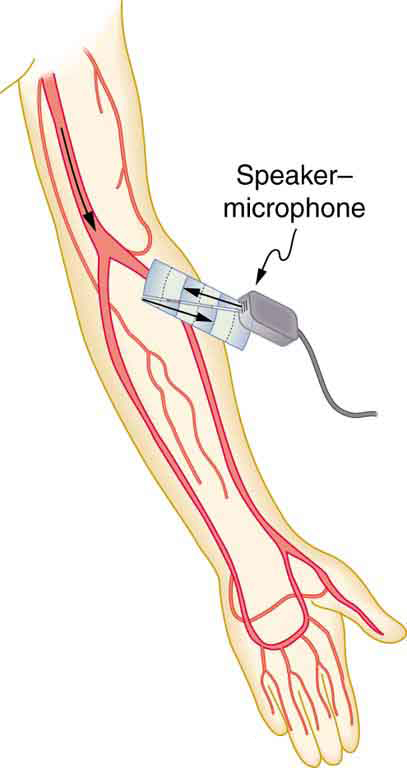
Ultrasound that has a frequency of 2.50 MHz is sent toward blood in an artery that is moving toward the source at 20.0 cm/s, as illustrated in [link] . Use the speed of sound in human tissue as 1540 m/s. (Assume that the frequency of 2.50 MHz is accurate to seven significant figures.)

1. What frequency does the blood receive?
2. What frequency returns to the source?
3. What beat frequency is produced if the source and returning frequencies are mixed?

Strategy

The first two questions can be answered using $f_{\text{obs}}=f_{\mathrm{s}}\left(\frac{v_{\mathrm{w}}}{v_{\mathrm{w}}\pm v_{\mathrm{s}}}\right)$ and $f_{\text{obs}}=f_{\mathrm{s}}\left(\frac{v_{\mathrm{w}}\pm v_{\text{obs}}}{v_{\mathrm{w}}}\right)$ for the Doppler shift. The last question asks for beat frequency, which is the difference between the original and returning frequencies.

Solution for (a)

(1) Identify knowns:

• The blood is a moving observer, and so the frequency it receives is given by
  $f_{\text{obs}}=f_{\mathrm{s}}\left(\frac{v_{\mathrm{w}}\pm v_{\text{obs}}}{v_{\mathrm{w}}}\right).$
• $v_{\mathrm{b}}$ is the blood velocity ( $v_{\text{obs}}$ here) and the plus sign is chosen because the motion is toward the source.

(2) Enter the given values into the equation.

(3) Calculate to find the frequency: 20,500,325 Hz.

Solution for (b)

(1) Identify knowns:

• The blood acts as a moving source.
• The microphone acts as a stationary observer.
• The frequency leaving the blood is 2,500,325 Hz, but it is shifted upward as given by
  $f_{\text{obs}}=f_{\mathrm{s}}\left(\frac{v_{\mathrm{w}}}{v_{\mathrm{w}}–v_{\mathrm{b}}}\right).$

  $f_{\mathrm{obs}}$ is the frequency received by the speaker-microphone.

• The source velocity is $v_{\mathrm{b}}$ .
• The minus sign is used because the motion is toward the observer.

The minus sign is used because the motion is toward the observer.

(2) Enter the given values into the equation:

(3) Calculate to find the frequency returning to the source: 2,500,649 Hz.

Solution for (c)

(1) Identify knowns:

• The beat frequency is simply the absolute value of the difference between $f_{\mathrm{s}}$ and $f_{\text{obs}}$ , as stated in:
  $f_{\mathrm{B}}=\mid f_{\text{obs}}-f_{\mathrm{s}}\mid .$

(2) Substitute known values:

(3) Calculate to find the beat frequency: 649 Hz.

Discussion

The Doppler shifts are quite small compared with the original frequency of 2.50 MHz. It is far easier to measure the beat frequency than it is to measure the echo frequency with an accuracy great enough to see shifts of a few hundred hertz out of a couple of megahertz. Furthermore, variations in the source frequency do not greatly affect the beat frequency, because both $f_{\mathrm{s}}$ and $f_{\text{obs}}$ would increase or decrease. Those changes subtract out in $f_{\mathrm{B}}=\mid f_{\text{obs}}-f_{\mathrm{s}}\mid .$