12.3 Parabolas

The definition of a parabola

Based on the discussion of circles, you might guess that the definition of a parabola will take the form: “The set of all points that...” and you would be correct. But the definition of a parabola is more complicated than that of a circle.

Definition of a parabola

In the text, you begin with a specific example of this process. The focus is (0,3) and the directrix is the line $y=\mathrm{–3}$ . If we use our “club” analogy again, we could say that this time, a point is a member of our club if its distance to (0,3) is the same as its distance to $y=\mathrm{–3}$ .

The resulting shape looks something like this:

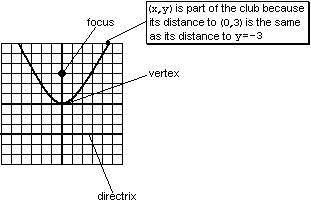
You may recall that a circle is entirely defined by its center—but the center is not, itself, a part of the circle. In a similar way, the focus and directrix define a parabola; but neither the focus, nor any point on the directrix, is a part of the parabola. The vertex, on the other hand—the point located directly between the focus and the directrix—is a part of the parabola.

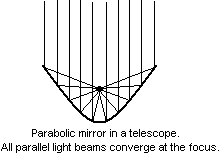
One of the obvious questions you might ask at this point is—who cares? It’s pretty obvious that circles come up a lot in the real world, but parabolas? It turns out that parabolas are more useful than you might think. For instance, many telescopes are based on parabolic mirrors. The reason is that all the light that comes in bounces off the mirror to the focus. The focus therefore becomes a point where you can see very dim, distant objects.

The formula of a parabola

We’ve already graphed parabolas in a previous chapter. As you may recall, we began with the simplest parabola, $y=x^2$ , and permuted it.

• $x^2+k$ moves it up by $k$
• $(x–h{)}^2$ moves it to the right by $h$
• Multiplying by a number in front stretches the graph vertically
• Multiplying by a negative number turns the graph upside-down.

Putting it all together, we arrive at:

Mathematical formula for a vertical parabola

Parabolas can also be horizontal . For the most part, the concepts are the same. The simplest horizontal parabola is $x=y^2$ , which has its vertex at the origin and opens to the right—from there, you can permute it. The directrix in this case is a vertical line.

Mathematical formula for a horizontal parabola

At this point, there are two useful exercises that you may want to try.

First, compare the two equations. How are they alike, and how are they different?

Second, consider the horizontal parabola equation as a set of permutations of the basic form $x=y^2$ . What is $k$ doing to the parabola, and why? How about $h$ , and $a$ ?