11.2 Simultaneity and time dilation  (Page 4/8)

Calculating $\mathrm{\Delta }t$ For a relativistic event: how long does a speedy muon live?

Suppose a cosmic ray colliding with a nucleus in the Earth’s upper atmosphere produces a muon that has a velocity $v=0\text{.}\text{950}c$ . The muon then travels at constant velocity and lives $1\text{.}\text{52}\mu \text{s}$ as measured in the muon’s frame of reference. (You can imagine this as the muon’s internal clock.) How long does the muon live as measured by an Earth-bound observer? (See [link] .)

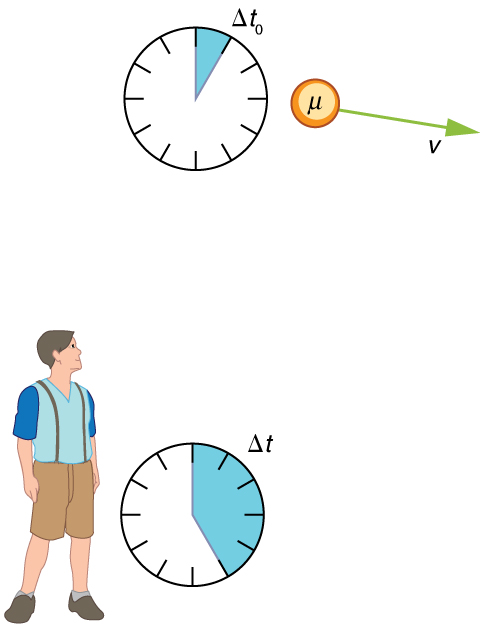
Strategy

A clock moving with the system being measured observes the proper time, so the time we are given is $\mathrm{\Delta }{t}_0=1\text{.}\text{52}\mu \text{s}$ . The Earth-bound observer measures $\mathrm{\Delta }t$ as given by the equation $\mathrm{\Delta }t={\gamma \mathrm{\Delta }t}_0$ . Since we know the velocity, the calculation is straightforward.

Solution

1) Identify the knowns. $v=0\text{.}\text{950}c$ , $\mathrm{\Delta }{t}_0=1\text{.}\text{52}\mu \text{s}$

2) Identify the unknown. $\mathrm{\Delta }t$

3) Choose the appropriate equation.

Use,

where

4) Plug the knowns into the equation.

First find $\gamma$ .

Use the calculated value of $\gamma$ to determine $\mathrm{\Delta }t$ .

Discussion

One implication of this example is that since $\gamma =3\text{.}\text{20}$ at $\text{95}\text{.}\mathrm{0\%}$ of the speed of light ( $v=0\text{.}\text{950}c$ ), the relativistic effects are significant. The two time intervals differ by this factor of 3.20, where classically they would be the same. Something moving at $0\text{.}\text{950}c$ is said to be highly relativistic.