| << Chapter < Page | Chapter >> Page > |
Name the ordered pair of each point shown:
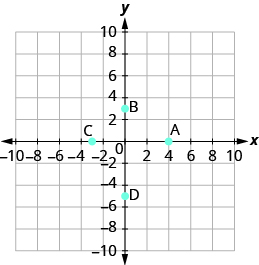
Name the ordered pair of each point shown:
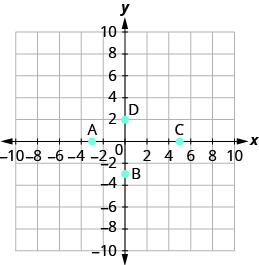
All the equations we solved so far have been equations with one variable. In almost every case, when we solved the equation we got exactly one solution . The process of solving an equation ended with a statement such as Then we checked the solution by substituting back into the equation.
Here’s an example of a linear equation in one variable , and its one solution.
But equations can have more than one variable. Equations with two variables can be written in the general form An equation of this form is called a linear equation in two variables.
An equation of the form where are not both zero, is called a linear equation in two variables.
Notice that the word “line” is in linear.
Here is an example of a linear equation in two variables, and
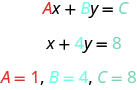
Is a linear equation? It does not appear to be in the form But we could rewrite it in this form.
|
| |
| Add to both sides. |
|
| Simplify. |
|
| Use the Commutative Property to put it in |
|
By rewriting as we can see that it is a linear equation in two variables because it can be written in the form
Linear equations in two variables have infinitely many solutions. For every number that is substituted for there is a corresponding value. This pair of values is a solution to the linear equation and is represented by the ordered pair When we substitute these values of and into the equation, the result is a true statement because the value on the left side is equal to the value on the right side.
An ordered pair is a solution to the linear equation if the equation is a true statement when the and of the ordered pair are substituted into the equation.
Determine which ordered pairs are solutions of the equation
Substitute the from each ordered pair into the equation and determine if the result is a true statement.
| ⓐ | ⓑ | ⓒ |
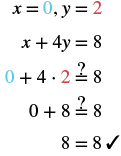 |
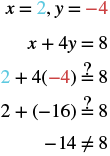 |
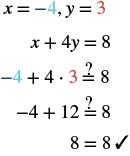 |
| is a solution. | is not a solution. | is a solution. |
Determine which ordered pairs are solutions to the given equation:
ⓐ , ⓒ
Determine which ordered pairs are solutions to the given equation:
ⓑ , ⓒ
Determine which ordered pairs are solutions of the equation.
Substitute the and from each ordered pair into the equation and determine if it results in a true statement.
| ⓐ | ⓑ | ⓒ |
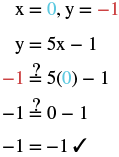 |
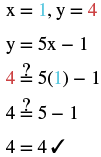 |
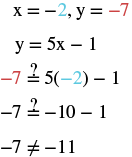 |
| is a solution. | is a solution. | is not a solution. |
Determine which ordered pairs are solutions of the given equation:
ⓑ
Determine which ordered pairs are solutions of the given equation:
ⓐ , ⓑ
In the previous examples, we substituted the of a given ordered pair to determine whether or not it was a solution to a linear equation. But how do we find the ordered pairs if they are not given? One way is to choose a value for and then solve the equation for Or, choose a value for and then solve for

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?