| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
The Quotient Property of Exponents , introduced in Divide Monomials , had two forms depending on whether the exponent in the numerator or denominator was larger.
If is a real number, and are whole numbers, then
What if we just subtract exponents, regardless of which is larger? Let’s consider
We subtract the exponent in the denominator from the exponent in the numerator.
We can also simplify by dividing out common factors:
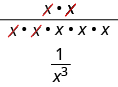
This implies that and it leads us to the definition of a negative exponent .
If is a positive integer and then
The negative exponent tells us to re-write the expression by taking the reciprocal of the base and then changing the sign of the exponent. Any expression that has negative exponents is not considered to be in simplest form. We will use the definition of a negative exponent and other properties of exponents to write an expression with only positive exponents.
Simplify:
| ⓐ | |
| Use the definition of a negative exponent, | |
| Simplify. |
| ⓑ | |
| Use the definition of a negative exponent, | |
| Simplify. |
When simplifying any expression with exponents, we must be careful to correctly identify the base that is raised to each exponent.
Simplify:
The negative in the exponent does not affect the sign of the base.
| ⓐ | |
| The exponent applies to the base, . | |
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. |
| ⓑ | |
| The expression
means "find the opposite of
".
The exponent applies only to the base, 3. |
|
| Rewrite as a product with −1. | |
| Take the reciprocal of the base and change the sign of the exponent. | |
| Simplify. |
We must be careful to follow the order of operations . In the next example, parts ⓐ and ⓑ look similar, but we get different results.
Simplify:
Remember to always follow the order of operations.
| ⓐ | |
| Do exponents before multiplication. | |
| Use | |
| Simplify. |
| ⓑ | |
| Simplify inside the parentheses first. | |
| Use | |
| Simplify. |
When a variable is raised to a negative exponent, we apply the definition the same way we did with numbers.
Simplify:
| Use the definition of a negative exponent, |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?