| << Chapter < Page | Chapter >> Page > |
When conducting a hypothesis test that compares two independent population proportions, the following characteristics should be present:
Comparing two proportions, like comparing two means, is common. If two estimated proportions are different, it may be due to a difference in the populations or it may be due to chance in the sampling. A hypothesis test can help determine if a difference in the estimated proportions reflects a difference in the population proportions.
Like the case of differences in sample means, we construct a sampling distribution for differences in sample proportions: where and are the sample proportions for the two sets of data in question. X A and X B are the number of successes in each group respectively, and n A and n B are the respective sample sizes from the two groups. Again we go the Central Limit theorem to find the distribution of this sampling distribution for the differences in sample proportions. And again we find that this sampling distribution, like the ones past, are normally distributed as proved by the Central Limit Theorem, as seen in [link] .

Generally, the null hypothesis allows for the test of a difference of a particular value, 𝛿 0 , just as we did for the case of differences in means.
Most common, however, is the test that the two proportions are the same. That is,
To conduct the test, we use a pooled proportion, p c .
where δ 0 is the hypothesized differences between the two proportions and p c is the pooled variance from formula above.
Two types of medication for poison ivy are being tested to determine if there is a difference in the proportions of adult patient reactions. Twenty out of a random sample of 200 adults given medication A still had poison ivy 30 minutes after taking the medication. Twelve out of another random sample of 200 adults given medication B still had itching 30 minutes after taking the medication. Test at a 10% level of significance.
The problem asks for a difference in proportions, making it a test of two proportions.
Let A and B be the subscripts for medication A and medication B, respectively. Then p A and p B are the population proportions.
The words "is a difference" tell you the test is two-tailed.
Distribution for the test: Since this is a test of two binomial population proportions, the distribution is normal:
( p′ A – p′ B ) = 0.04 follows an approximate normal distribution.
Estimated proportion for group A:
Estimated proportion for group B:
The estimated difference between the two groups is :
p′
A –
p′
B = 0.1 – 0.06 = 0.04.
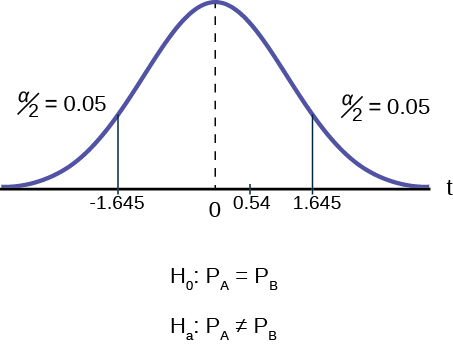
The calculated test statistic is .54 and is not in the tail of the distribution.
Make a decision: Since the calculate test statistic is not in the tail of the distribution we cannot reject H 0 .
Conclusion: At a 1% level of significance, from the sample data, there is not sufficient evidence to conclude that there is a difference in the proportions of adult patients who did not react after 30 minutes to medication A and medication B .

Notification Switch
Would you like to follow the 'Introductory statistics' conversation and receive update notifications?