10.1 Centripetal acceleration  (Page 36/6)

We know from kinematics that acceleration is a change in velocity, either in its magnitude or in its direction, or both. In uniform circular motion, the direction of the velocity changes constantly, so there is always an associated acceleration, even though the magnitude of the velocity might be constant. You experience this acceleration yourself when you turn a corner in your car. (If you hold the wheel steady during a turn and move at constant speed, you are in uniform circular motion.) What you notice is a sideways acceleration because you and the car are changing direction. The sharper the curve and the greater your speed, the more noticeable this acceleration will become. In this section we examine the direction and magnitude of that acceleration.

[link] shows an object moving in a circular path at constant speed. The direction of the instantaneous velocity is shown at two points along the path. Acceleration is in the direction of the change in velocity, which points directly toward the center of rotation (the center of the circular path). This pointing is shown with the vector diagram in the figure. We call the acceleration of an object moving in uniform circular motion (resulting from a net external force) the centripetal acceleration    ( $a_{\text{c}}$ ); centripetal means “toward the center” or “center seeking.”

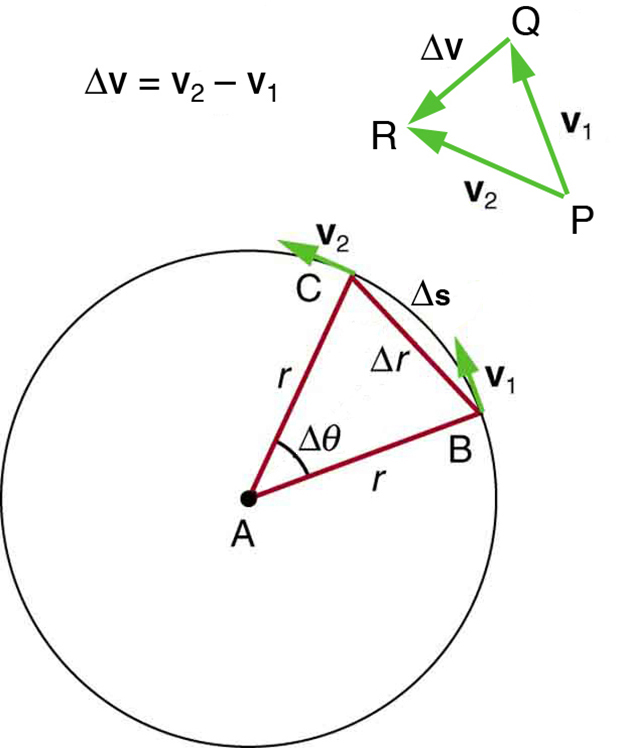
The direction of centripetal acceleration is toward the center of curvature, but what is its magnitude? Note that the triangle formed by the velocity vectors and the one formed by the radii $r$ and $\text{Δ}s$ are similar. Both the triangles ABC and PQR are isosceles triangles (two equal sides). The two equal sides of the velocity vector triangle are the speeds $v_1=v_2=v$ . Using the properties of two similar triangles, we obtain

Acceleration is $\text{Δ}v/\text{Δ}t$ , and so we first solve this expression for $\text{Δ}v$ :

Then we divide this by $\text{Δ}t$ , yielding

Finally, noting that $\text{Δ}v/\text{Δ}t=a_{\text{c}}$ and that $\text{Δ}s/\text{Δ}t=v$ , the linear or tangential speed, we see that the magnitude of the centripetal acceleration is

which is the acceleration of an object in a circle of radius $r$ at a speed $v$ . So, centripetal acceleration is greater at high speeds and in sharp curves (smaller radius), as you have noticed when driving a car. But it is a bit surprising that $a_{\text{c}}$ is proportional to speed squared, implying, for example, that it is four times as hard to take a curve at 100 km/h than at 50 km/h. A sharp corner has a small radius, so that $a_{\text{c}}$ is greater for tighter turns, as you have probably noticed.

It is also useful to express $a_{\text{c}}$ in terms of angular velocity. Substituting $v=\mathrm{r\omega }$ into the above expression, we find $a_{\text{c}}={\left(\mathrm{r\omega }\right)}^2/r={\mathrm{r\omega }}^2$ . We can express the magnitude of centripetal acceleration using either of two equations: