10.1 Centripetal acceleration  (Page 2/6)

How does the centripetal acceleration of a car around a curve compare with that due to gravity?

What is the magnitude of the centripetal acceleration of a car following a curve of radius 500 m at a speed of 25.0 m/s (about 90 km/h)? Compare the acceleration with that due to gravity for this fairly gentle curve taken at highway speed. See [link] (a).

Strategy

Because $v$ and $r$ are given, the first expression in $a_{\text{c}}=\frac{v^2}{r}\mathrm{; }{a}_{\text{c}}={\mathrm{r\omega }}^2$ is the most convenient to use.

Solution

Entering the given values of $v=\text{25}\text{.}0\text{m/s}$ and $r=\text{500 m}$ into the first expression for $a_{\text{c}}$ gives

Discussion

To compare this with the acceleration due to gravity $(g=9\text{.}80{\text{m/s}}^2)$ , we take the ratio of $a_{\text{c}}/g=\left(1\text{.}\text{25}{\text{m/s}}^2\right)/\left(9\text{.}\text{80}{\text{m/s}}^2\right)=0\text{.}\text{128}$ . Thus, $a_{\text{c}}=0\text{.}\text{128 g}$ and is noticeable especially if you were not wearing a seat belt.

How big is the centripetal acceleration in an ultracentrifuge?

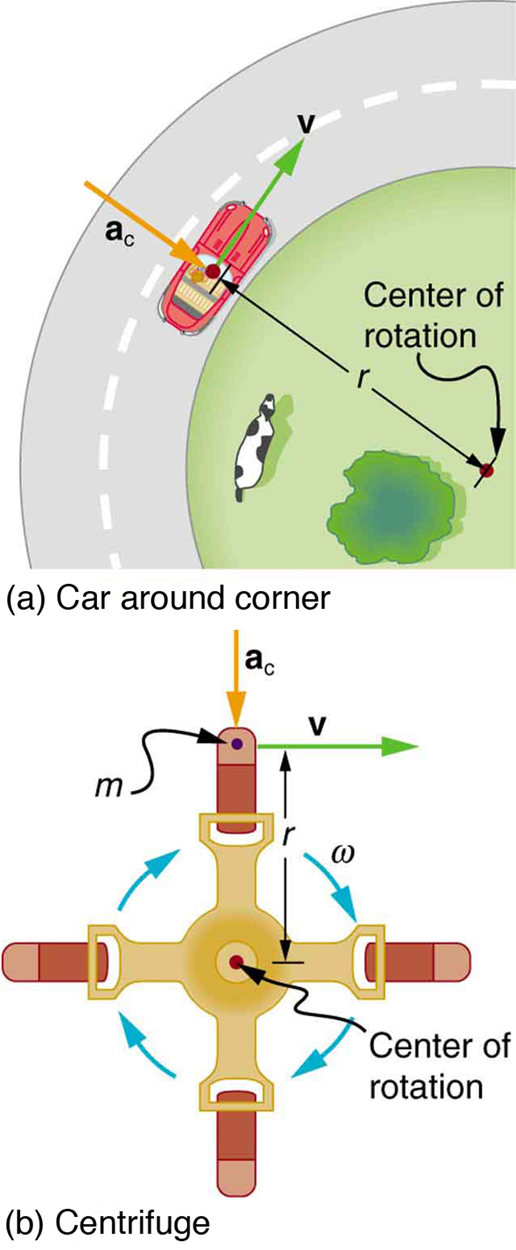
Calculate the centripetal acceleration of a point 7.50 cm from the axis of an ultracentrifuge    spinning at ${\text{7.5 × 10}}^{\text{4}}\text{rev/min.}$ Determine the ratio of this acceleration to that due to gravity. See [link] (b).

Strategy

The term rev/min stands for revolutions per minute. By converting this to radians per second, we obtain the angular velocity $\omega$ . Because $r$ is given, we can use the second expression in the equation $a_{\text{c}}=\frac{v^2}{r};a_{\text{c}}={\mathit{r\omega }}^2$ to calculate the centripetal acceleration.

Solution

To convert $7\text{.}\text{50}\times {\text{10}}^4\text{rev}/\text{min}$ to radians per second, we use the facts that one revolution is $\mathrm{2\pi }\text{rad}$ and one minute is 60.0 s. Thus,

Now the centripetal acceleration is given by the second expression in $a_{\text{c}}=\frac{v^2}{r}\mathrm{; }{a}_{\text{c}}={\mathrm{r\omega }}^2$ as

Converting 7.50 cm to meters and substituting known values gives

Note that the unitless radians are discarded in order to get the correct units for centripetal acceleration. Taking the ratio of $a_{\text{c}}$ to $g$ yields

Discussion

This last result means that the centripetal acceleration is 472,000 times as strong as $g$ . It is no wonder that such high $\omega$ centrifuges are called ultracentrifuges. The extremely large accelerations involved greatly decrease the time needed to cause the sedimentation of blood cells or other materials.