1.4 Difference of sets  (Page 3/2)

We can extend the concept of subtraction, used in algebra, to the sets. If a set “B” is subtracted from set “A”, the resulting difference set consists of elements, which are exclusive to set “A”. We represent the symbol of difference of sets as “A-B” and pronounce the same as “A minus B”.

Difference of sets

The difference of sets “A-B” is the set of all elements of “A”, which do not belong to “B”.

In the set builder form, the difference set is :

$$A-B=\{x:x\in Aandx\notin B\}$$

and

$$B-A=\{x:x\in Bandx\notin A\}$$

On Venn’s diagram, the difference "A-B" is the region of “A”, which excludes the common region with set “B”.

Difference of two sets

Interpretation of difference set

Let us examine the defining set of intersection :

$$A-B=\{x:x\in Aandx\notin B\}$$

We consider an arbitrary element, say “x”, of the difference set. Then, we interpret the conditional meaning as :

$$Ifx\in A-B\Rightarrow x\in Aandx\notin B.$$

The conditional statement is true in opposite direction as well. Hence,

$$Ifx\in Aandx\notin B\Rightarrow x\in A-B.$$

We can summarize two statements with two ways arrow as :

$$Ifx\in A-B\iff x\in Aandx\notin B.$$

Composition of a set

From Venn’s diagram, we observe that if we derive union of ( $A\cap B$ ) to either of the difference sets, then we get the complete individual set.

Difference of two sets

$$A=\left(A-B\right)\cup \left(A\cap B\right)$$

and

$$B=\left(B-A\right)\cup \left(A\cap B\right)$$

Difference of sets is not commutative

The positions of sets about minus operator affect the result. It is clear from the figure above, where “A-B” and “B-A” represent different regions on Venn’s diagram. As such, the difference of sets is not commutative. Let us consider the example used earlier, where :

$$A=\left\{\mathrm{1,2,3,4,5,6}\right\}$$

$$A=\left\{\mathrm{4,5,6,7,8}\right\}$$

Then,

$$\Rightarrow A-B=\left\{\mathrm{1,2,3}\right\}$$

and

$$\Rightarrow B-A=\left\{\mathrm{7,8}\right\}$$

Clearly,

$$\Rightarrow A-B\ne B-A$$

Symmetric difference

From the Venn’s diagram, we can see that union of two sets is equal to three distinct regions. Alternatively, we can say that the region represented by the union of two sets is equal to the sum of the regions representing three “disjoint” sets (i) difference set A-B (ii) intersection set " $A\cap B$ " and (iii) difference set B-A.

Difference of two sets

We use the term “symmetric set” for combining two differences as marked on Venn’s diagram. It is denoted as “ $A\text{Δ}B$ ”.

$$A\text{Δ}B=\left(A-B\right)\cup \left(B-A\right)$$

Complement of a set

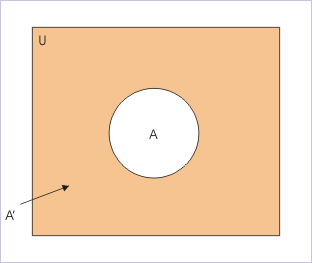
The complement is a special case of the difference operation. The set in question is subtracted from universal set, “U”. Thus, one of the sets in difference operation is fixed. We define complement of a set as its difference with universal set, "U". The complement of a set is denoted by the same symbol as that of set, but with an apostrophe. Hence, complement of set A is set A’.

Complement of a set

The complement of a set “A” consists of elements, which are elements of “U”, but not the elements of “A”.

We write the complement set in terms of set builder form as :

$$A\prime =\{x:x\in Uandx\notin A\}$$

Note that elements of A’ does not belong to set “A”. On Venn’s diagram, the complement of “A” is the remaining region of the universal set.

Complement of a set