1.4 Area and arc length in polar coordinates

In the rectangular coordinate system, the definite integral provides a way to calculate the area under a curve. In particular, if we have a function $y=f(x)$ defined from $x=a$ to $x=b$ where $f\left(x\right)>0$ on this interval, the area between the curve and the x -axis is given by $A={\displaystyle {\int }_a^{b}f\left(x\right)dx}.$ This fact, along with the formula for evaluating this integral, is summarized in the Fundamental Theorem of Calculus. Similarly, the arc length of this curve is given by $L={\displaystyle {\int }_a^b\sqrt{1+{\left(f^{\prime }\left(x\right)\right)}^2}dx}.$ In this section, we study analogous formulas for area and arc length in the polar coordinate system.

Areas of regions bounded by polar curves

We have studied the formulas for area under a curve defined in rectangular coordinates and parametrically defined curves. Now we turn our attention to deriving a formula for the area of a region bounded by a polar curve. Recall that the proof of the Fundamental Theorem of Calculus used the concept of a Riemann sum to approximate the area under a curve by using rectangles. For polar curves we use the Riemann sum again, but the rectangles are replaced by sectors of a circle.

Consider a curve defined by the function $r=f\left(\theta \right),$ where $\alpha \le \theta \le \beta .$ Our first step is to partition the interval $[\alpha ,\beta ]$ into n equal-width subintervals. The width of each subinterval is given by the formula $\text{Δ}\theta =(\beta -\alpha )\text{/}n,$ and the i th partition point ${\theta }_i$ is given by the formula ${\theta }_i=\alpha +i\text{Δ}\theta .$ Each partition point $\theta ={\theta }_i$ defines a line with slope $\text{tan}{\theta }_i$ passing through the pole as shown in the following graph.

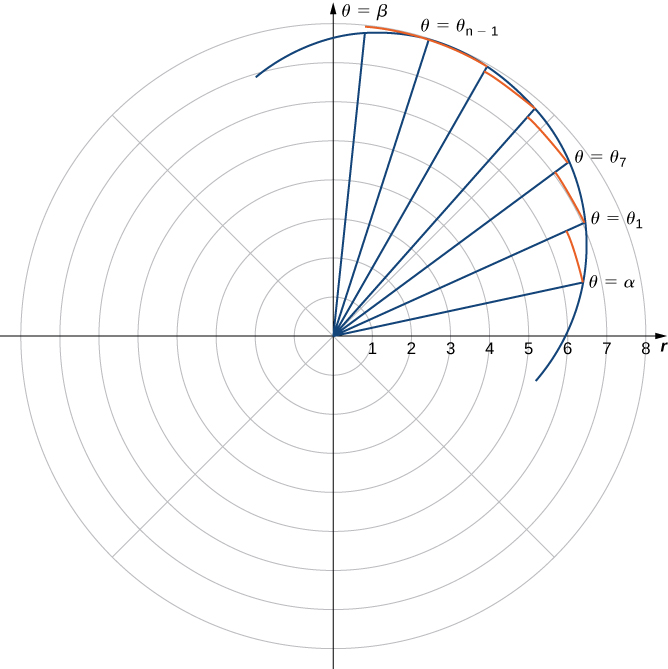
The line segments are connected by arcs of constant radius. This defines sectors whose areas can be calculated by using a geometric formula. The area of each sector is then used to approximate the area between successive line segments. We then sum the areas of the sectors to approximate the total area. This approach gives a Riemann sum approximation for the total area. The formula for the area of a sector of a circle is illustrated in the following figure.

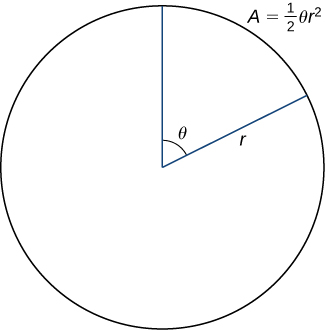
Recall that the area of a circle is $A=\pi r^2.$ When measuring angles in radians, 360 degrees is equal to $2\pi$ radians. Therefore a fraction of a circle can be measured by the central angle $\theta .$ The fraction of the circle is given by $\frac{\theta }{2\pi },$ so the area of the sector is this fraction multiplied by the total area:

Since the radius of a typical sector in [link] is given by $r_i=f\left({\theta }_i\right),$ the area of the i th sector is given by

Therefore a Riemann sum that approximates the area is given by

We take the limit as $n\to \infty$ to get the exact area:

This gives the following theorem.

Finding an area of a polar region

Find the area of one petal of the rose defined by the equation $r=3\text{sin}\left(2\theta \right).$

The graph of $r=3\text{sin}\left(2\theta \right)$ follows.

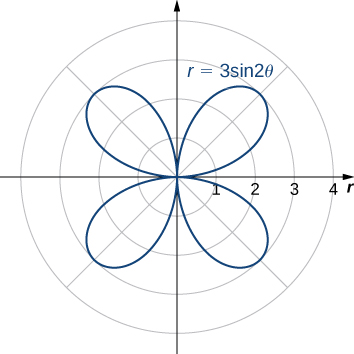
When $\theta =0$ we have $r=3\text{sin}\left(2(0)\right)=0.$ The next value for which $r=0$ is $\theta =\pi \text{/}2.$ This can be seen by solving the equation $3\text{sin}(2\theta )=0$ for $\theta .$ Therefore the values $\theta =0$ to $\theta =\pi \text{/}2$ trace out the first petal of the rose. To find the area inside this petal, use [link] with $f\left(\theta \right)=3\text{sin}\left(2\theta \right),$ $\alpha =0,$ and $\beta =\pi \text{/}2\text{:}$

$\begin{array}{cc}\hfill A& =\frac{1}{2}{\displaystyle {\int }_{\alpha }^{\beta }{\left[f\left(\theta \right)\right]}^{2}d\theta }\hfill \\ & =\frac{1}{2}{\displaystyle {\int }_0^{\pi \text{/}2}{\left[3\text{sin}\left(2\theta \right)\right]}^{2}d\theta }\hfill \\ & =\frac{1}{2}{\displaystyle {\int }_0^{\pi \text{/}2}9{\text{sin}}^2\left(2\theta \right)d\theta }.\hfill \end{array}$

To evaluate this integral, use the formula ${\text{sin}}^2\alpha =\left(1-\text{cos}(2\alpha )\right)\text{/}2$ with $\alpha =2\theta \text{:}$

$\begin{array}{cc}\hfill A& =\frac{1}{2}{\displaystyle {\int }_0^{\pi \text{/}2}9{\text{sin}}^2\left(2\theta \right)d\theta }\hfill \\ & =\frac{9}{2}{\displaystyle {\int }_0^{\pi \text{/}2}\frac{\left(1-\text{cos}\left(4\theta \right)\right)}{2}d\theta }\hfill \\ & =\frac{9}{4}\left({\displaystyle {\int }_0^{\pi \text{/}2}1-\text{cos}\left(4\theta \right)d\theta }\right)\hfill \\ & =\frac{9}{4}{(\theta -\frac{\text{sin}\left(4\theta \right)}{4}|}_0^{\pi \text{/}2}\hfill \\ & =\frac{9}{4}\left(\frac{\pi }{2}-\frac{\text{sin}2\pi }{4}\right)-\frac{9}{4}\left(0-\frac{\text{sin}4\left(0\right)}{4}\right)\hfill \\ & =\frac{9\pi }{8}.\hfill \end{array}$

Got questions? Get instant answers now!

Got questions? Get instant answers now!