| << Chapter < Page | Chapter >> Page > |
We can derive some useful identities from the six trigonometric functions. The other four trigonometric functions can be related back to the sine and cosine functions using these basic relationships:
Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.
Evaluate
Simplify
We can simplify this by rewriting both functions in terms of sine and cosine.
By showing that can be simplified to we have, in fact, established a new identity.
Simplify
We can use these fundamental identities to derive alternative forms of the Pythagorean Identity , One form is obtained by dividing both sides by
The other form is obtained by dividing both sides by
If and is in quadrant IV, as shown in [link] , find the values of the other five trigonometric functions.
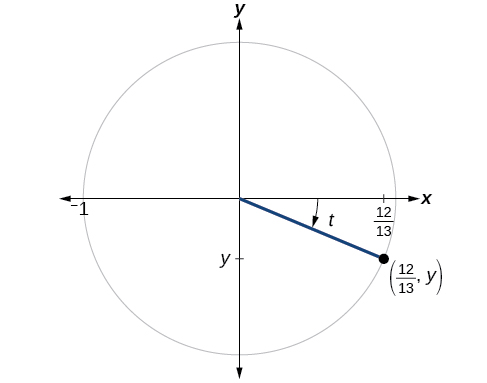
We can find the sine using the Pythagorean Identity, and the remaining functions by relating them to sine and cosine.
The sign of the sine depends on the y -values in the quadrant where the angle is located. Since the angle is in quadrant IV, where the y -values are negative, its sine is negative,
The remaining functions can be calculated using identities relating them to sine and cosine.
If and find the values of the other five functions.
As we discussed in the chapter opening, a function that repeats its values in regular intervals is known as a periodic function . The trigonometric functions are periodic. For the four trigonometric functions, sine, cosine, cosecant and secant, a revolution of one circle, or will result in the same outputs for these functions. And for tangent and cotangent, only a half a revolution will result in the same outputs.

Notification Switch
Would you like to follow the 'Essential precalculus, part 2' conversation and receive update notifications?