| << Chapter < Page | Chapter >> Page > |
Convert into polar coordinates and into rectangular coordinates.
and
The polar representation of a point is not unique. For example, the polar coordinates and both represent the point in the rectangular system. Also, the value of can be negative. Therefore, the point with polar coordinates also represents the point in the rectangular system, as we can see by using [link] :
Every point in the plane has an infinite number of representations in polar coordinates. However, each point in the plane has only one representation in the rectangular coordinate system.
Note that the polar representation of a point in the plane also has a visual interpretation. In particular, is the directed distance that the point lies from the origin, and measures the angle that the line segment from the origin to the point makes with the positive -axis. Positive angles are measured in a counterclockwise direction and negative angles are measured in a clockwise direction. The polar coordinate system appears in the following figure.
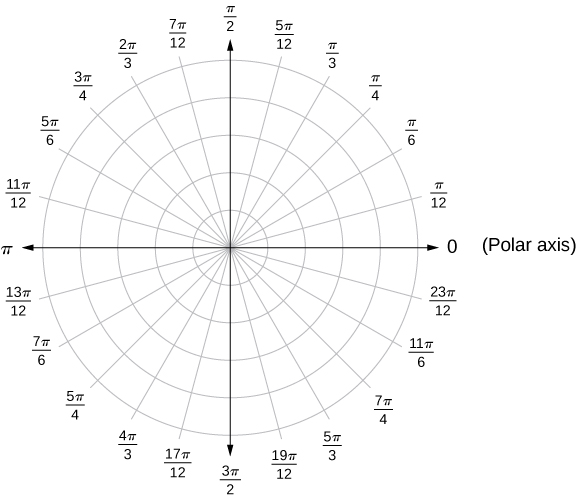
The line segment starting from the center of the graph going to the right (called the positive x -axis in the Cartesian system) is the polar axis . The center point is the pole , or origin, of the coordinate system, and corresponds to The innermost circle shown in [link] contains all points a distance of 1 unit from the pole, and is represented by the equation Then is the set of points 2 units from the pole, and so on. The line segments emanating from the pole correspond to fixed angles. To plot a point in the polar coordinate system, start with the angle. If the angle is positive, then measure the angle from the polar axis in a counterclockwise direction. If it is negative, then measure it clockwise. If the value of is positive, move that distance along the terminal ray of the angle. If it is negative, move along the ray that is opposite the terminal ray of the given angle.
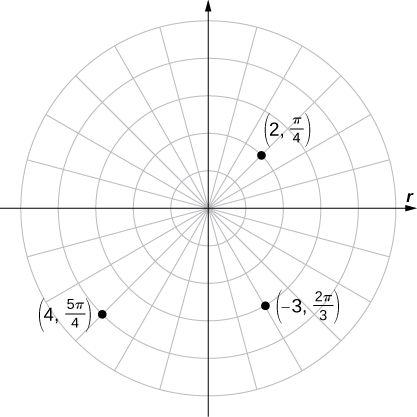
Plot each of the following points on the polar plane.
The three points are plotted in the following figure.
Now that we know how to plot points in the polar coordinate system, we can discuss how to plot curves. In the rectangular coordinate system, we can graph a function and create a curve in the Cartesian plane. In a similar fashion, we can graph a curve that is generated by a function
The general idea behind graphing a function in polar coordinates is the same as graphing a function in rectangular coordinates. Start with a list of values for the independent variable in this case) and calculate the corresponding values of the dependent variable This process generates a list of ordered pairs, which can be plotted in the polar coordinate system. Finally, connect the points, and take advantage of any patterns that may appear. The function may be periodic, for example, which indicates that only a limited number of values for the independent variable are needed.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?